엔지니어가 되고 싶은 공돌이
08. 비선형방정식 - 1(Non-Linear Equation - 1) 본문

8. 1. 이분법(Bisection Method)
- 5차 이상의 방정식은 그 미만의 방정식들처럼 대수적으로 해를 구할 수 없다. 일반적으로 근사해를 구해서 사용한다.
- 중간값 정리(Intermediate Value Theorem): 함수 f(x)가 [a, b]에서 연속이고, f(a)f(b) < 0 이면 f(x) = 0을 만족하는 근이 (a, b)에 적어도 하나 있다.
- Bisection Method Algorithm.
f(a)f(b) < 0 을 만족하는 구간 [a, b]를 초기값으로 잡는다.
for n = 1, 2, ….
1) c = (a + b) / 2.
2) 만약 | f(c) | ≤ ε or |b - c| ≤ ε 이면 반복을 중지한다.
3) f(a)f(c) ≤ 0 이면 a = a, b = c 로 정한다.
f(a)f(c) > 0 이면 a = c, b = b 로 정한다.

8. 2. 오차조정법(Regular-Falsi Method)
- 이분법보다 좀 더 빠른 방법이다. 다만, 이분법은 반드시 해를 구할 수 있다.
- Regular-Falsi Method: 두 점을 직나는 직선이 x축과 만나는 교점을 이용.
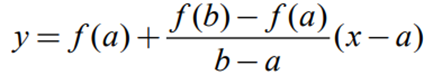
- x축과 만나는 교점이므로 y = 0.
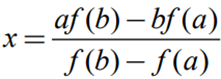
- x가 새로운 점 c가 된다.
- Regular-Falsi Method Algorithm.
f(a)f(b) < 0 을 만족하는 구간 [a, b]를 초기값으로 잡는다.
for n = 1, 2, ….
1) x축과 만나는 점 c를 구한다.
2) f(a)f(c) < 0 이면 b = c 로 놓는다. f(a)f(c) > 0 이면 a = c로 놓는다.
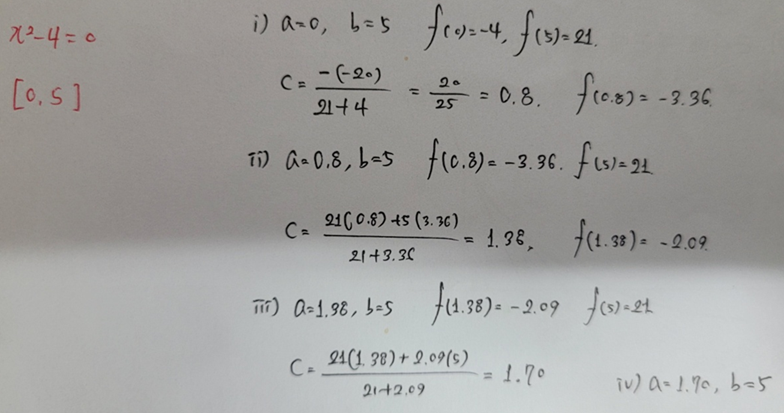
'Mathematics > Numerical Analysis' 카테고리의 다른 글
| 10. 라그랑주 보간법(Lagrange Interpolation) (0) | 2024.07.12 |
|---|---|
| 09. 비선형방정식 -2 (Non-Linear Equation - 2) (2) | 2024.07.12 |
| 07. 고유값, 고유벡터, 거듭제곱방법(Eigenvalue and Eigenvector and Power Method) (0) | 2024.07.12 |
| 06. 선형방정식의 반복법(Iteration Method of Linear Equation) (0) | 2024.07.12 |
| 05. 노름(Norm) (0) | 2024.07.12 |




