엔지니어가 되고 싶은 공돌이
09. 비선형방정식 -2 (Non-Linear Equation - 2) 본문

9. 1. 뉴턴법(Newton Method)

- Newton Method는 초기값이 근에 충분히 가까이 있다면 항상 수렴한다. 그러나 초기값이 멀리 떨어져 있다면 수렴이 보장되지 않고 발산하거나 진동할 수 있다.

9. 2. 할선법(Secant Method)
- Secant Method: f’(x) 대신 xn 과 xn-1 의 평균변화률을 이용한다.
- 2개의 초기값이 필요하고, Newton Method에 비해 수렴속도가 느리다.
- 초기값이 근에 가까이 있지 않다면 수렴이 보장되지 않는다.

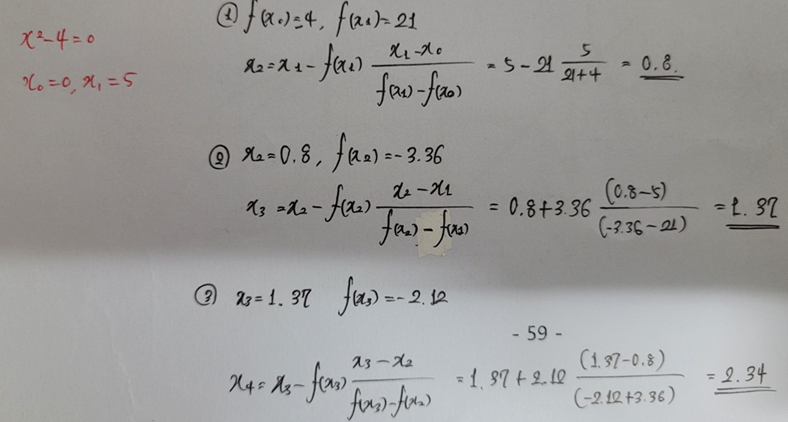
9. 3. 고정점 반복법(Fixed Point Iteration)
- f(x) = 0의 해를 구하는 문제를 여러가지 방법으로 적당한 함수 g(x)(기존 f(x)에서 x에 대하여 정리)를 택하여서 x = g(x)의 해를 구하는 문제로 바꿀 수 있다.
- p = g(p)가 되는 p를 함수 g(x)의 고정점(fixed point), 함수 g(x)를 반복함수(Iteration Function)라 한다.
- 함수 g(x)와 초기값 x0의 선택에 따라 Fixed Point Iteration의 결과가 달라질 수 있다.
- 고정점 정리(Fixid Point Theorem).
[a, b]에서 함수가 연속이고, 미분가능하며, |g’(a)| < 1 이고, |g’(b)| < 1 이면 임의의 초기값 x0에 대하여
xn+1 = g(xn) 은 Fixid Point p에 수렴한다.

'Mathematics > Numerical Analysis' 카테고리의 다른 글
| 11. 뉴턴의 분할차분법(Newton’s Interpolator Divided Difference Formula) (0) | 2024.07.12 |
|---|---|
| 10. 라그랑주 보간법(Lagrange Interpolation) (0) | 2024.07.12 |
| 08. 비선형방정식 - 1(Non-Linear Equation - 1) (0) | 2024.07.12 |
| 07. 고유값, 고유벡터, 거듭제곱방법(Eigenvalue and Eigenvector and Power Method) (0) | 2024.07.12 |
| 06. 선형방정식의 반복법(Iteration Method of Linear Equation) (0) | 2024.07.12 |
Comments




