엔지니어가 되고 싶은 공돌이
07. 고유값, 고유벡터, 거듭제곱방법(Eigenvalue and Eigenvector and Power Method) 본문
07. 고유값, 고유벡터, 거듭제곱방법(Eigenvalue and Eigenvector and Power Method)
Geca 2024. 7. 12. 13:36
7. 1. 고유값과 고유벡터(Eigenvalue and Eigenvector)
- Ax = λx 를 만족하는 0이 아닌 벡터가 존재하면, Scalar λ를 A의 고유값(Eigenvalue)라 부르고, x를 λ에 대응하는 A의 고유벡터(Eigenvector)라 부른다.
- 고유공간(Eigenspace): 영 벡터와 고유값 λ에 대응하는 모든 고유벡터의 집합.
1) 고유값 계산(Eigenvalue Calculation).
- 고유방정식(= 특성방정식, Characteristic Equation): det(A - λI) = 0.
- 고유방정식의 해가 Eigenvalue이다.
2) 고유벡터 계산(Eigenvector Calculation).
- (A - λiI)x = 0에 대응하는 벡터 x.
- Properties of Eigenvalue and Eigenvector.
1) 크기가 n인 행렬은 중복을 포함해서 복소수 범위내에서 Eigenvalue n개를 갖는다.
2) 크기가 n인 행렬이 서로 다른 n개의 Eigenvalue을 가지면 그에 대응하는 Eigenvector는 독립이다.
3) Upper(Lower) Triangular Matrix의 Eigenvalue는 행렬의 대각성분과 같다.
4) Symmetric Matrix의 Eigenvalue가 다르면, 그에 대응하는 Eigenvector는 Orthogonal한다.
5) Matrix A가 Symmetric이면 A의 Eigenvalue는 Real Number이다.
6) Matrix A의 Eigenvalue λ는 - || A || ≤ λ ≤ || A || 이다.

7. 2. 거듭제곱방법(Power Method)
- Characteristic Equation으로 Eigenvalue를 구할 때, 행렬의 크기가 커질수록 행렬식의 오차가 커지게 된다.
- 실제 응용에서는 절대값이 가장 큰 Eigenvalue가 중요한 역할을 하게 된다.
- Power Method: 절대값이 가장 큰 고유값(Dominant Eigenvalue)과 고유벡터를 반복법으로 구하는 방법.
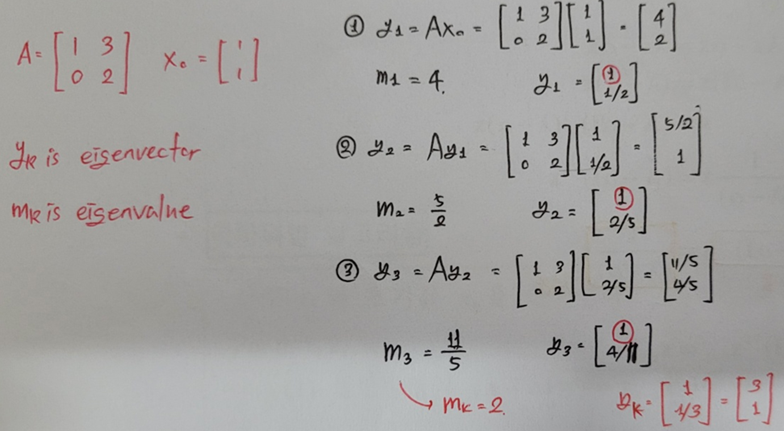
7. 3. 역거듭제곱방법(Inverse Power Method)
- Inverse Power Method: 임의의 상수 a에 가장 가까운 Eigenvalue를 구하는 방법이다.
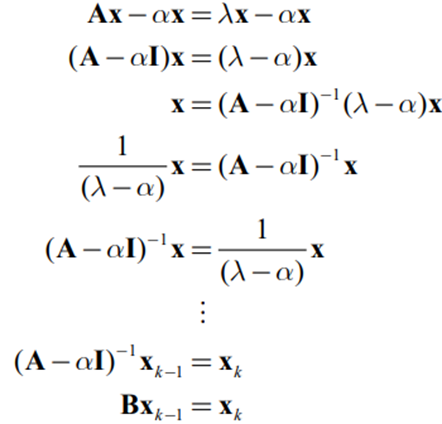
- Matrix A가 Eigenvalue λ와 이에 대응하는 Eigenvector x를 가지면 임의의 수 a ≠ λ에 대해 Matrix (A-aI)-1은 Eigenvalue 1/(λ - a) 와 Eigenvector x를 가진다.
'Mathematics > Numerical Analysis' 카테고리의 다른 글
| 09. 비선형방정식 -2 (Non-Linear Equation - 2) (2) | 2024.07.12 |
|---|---|
| 08. 비선형방정식 - 1(Non-Linear Equation - 1) (0) | 2024.07.12 |
| 06. 선형방정식의 반복법(Iteration Method of Linear Equation) (0) | 2024.07.12 |
| 05. 노름(Norm) (0) | 2024.07.12 |
| 04. LU 분해법과 숄레스키 방법(LU Decomposition Method and Cholesky Method) (0) | 2024.07.12 |




