엔지니어가 되고 싶은 공돌이
10. 라그랑주 보간법(Lagrange Interpolation) 본문

10. 1. 라그랑주 보간법(Lagrange Interpolation)
- Interpolation: 주어진 자료를 만족하는 함수 P(x)를 찾고, 자료에 없는 새로운 점 x_bar 에서 기대값 P(x_bar) 를 찾는 방법.
1) 서로 다른 n + 1개의 점을 지나는 n차 다항식(nth Degree Polynomial)은 단 1개 존재한다.
(x0, y0), (x1, y1)으로 유일한 1차 다항식을 구할 수 있다.

(x0, y0), (x1, y1), (x2, y2) 으로 유일한 2차 다항식을 구할 수 있다.
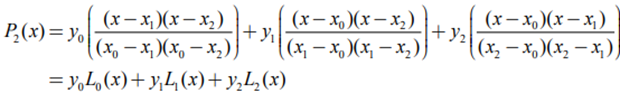
2) 서로 다른 n + 1개의 점을 지나는 n차 보간 다항식(nth Degree Interpolation Polynomial)은
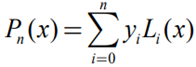

- 라그랑주 보간법의 장단점(pros and cons of Lagrange interpolation)
1) 라그랑주 보간법은 간편하다는 장점이 있지만, 새로운 점을 추가할 때 이전의 계산정보를 활용하기 어렵다는 단점을 가지고 있다.
2) 차수가 크면, 오차가 커질 수 있으므로 낮은 차수에 적합하다.
'Mathematics > Numerical Analysis' 카테고리의 다른 글
| 12. 스플라인 함수(Spline Function) (1) | 2024.07.12 |
|---|---|
| 11. 뉴턴의 분할차분법(Newton’s Interpolator Divided Difference Formula) (0) | 2024.07.12 |
| 09. 비선형방정식 -2 (Non-Linear Equation - 2) (2) | 2024.07.12 |
| 08. 비선형방정식 - 1(Non-Linear Equation - 1) (0) | 2024.07.12 |
| 07. 고유값, 고유벡터, 거듭제곱방법(Eigenvalue and Eigenvector and Power Method) (0) | 2024.07.12 |
Comments




