엔지니어가 되고 싶은 공돌이
10. 연속확률변수(Continuous Random Variable) 본문

10. 1. 균등분포(Uniform Distribution)
- 두 점 a, b (a < b)사이에서 p.d.f 가 일정하게 나타나는 확률변수.
- X ~ U(a, b).

- Mean: (a + b)/2, Variance: (b - a)2 / 12.
- 누적분포함수(Culmulative Distribution Function)

10. 2. 지수분포(Exponential Distribution)
- 관심의 대상이 되는 사건이 처음 발생할 때까지 걸리는 시간에 관한 확률분포.
- 관심의 대상이 되는 사건이 처음 발생할 때까지의 횟수는 Geometric Distribution이다.
- 관심의 대상이 되는 사건이 단위 시간동안 일어나는 사건들의 숫자에 관련된 확률분포는 Poisson Distribution 이
고, Exponential Distribution은 사건들이 일어나는 사이에 걸리는 시간과 관련된 것이다.
- X ~ Exp(λ).
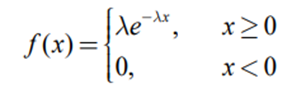
- Mean: 1 / λ, Variance: 1 / λ2.
- 누적분포함수(Culmulative Distribution Function)
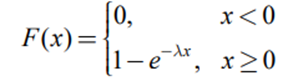
- 생존함수(Survival Function)
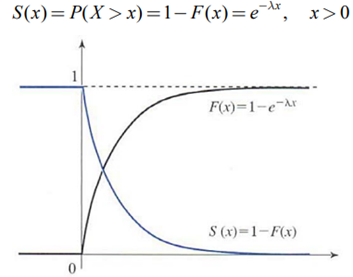
- 비기억성성질(Memorylessness Property)
P(X > a + b | X > a) = P(X > b).
과거의 사건이 미래에 영향을 끼치지 못한다는 의미를 가진다.
10. 3. 감마분포(Gamma Distribution)
- 관심의 대상이 되는 사건이 n번 발생할 떄까지 걸리는 전체 시간에 관한 확률분포.
- X ~ Γ(α, β).
- α는 n번의 횟수를, β는 1/λ(Exponential Distribution) = 1/m(Poisson Distribution)을 의미한다.
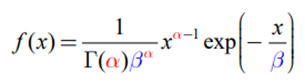
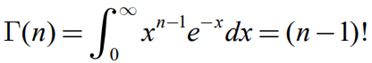
- α(형상모수, Shape Parameter): Gamma Distribution의 모양을 결정하며, α가 커짐에 따라 곡선의 꼭짓점이 원점에서 멀어진다.
- β(척도모수, Scale Parameter): 흩어진 정도를 나타내며, β가 작을수록 밀집정도가 좁아진다.
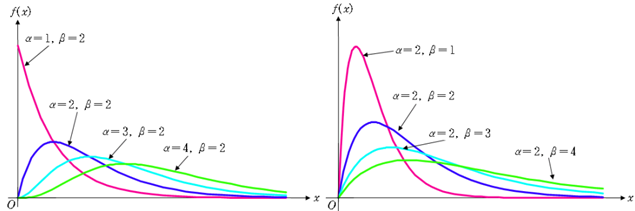
- 감마함수의 성질(Properties of Gamma Function)
1) Γ(1) = 1.
2) Γ(α + 1) = αΓ(α).
3) Γ(n + 1) = nΓ(n) = n!.
4) Γ(1/2) = √π.
- mean: αβ, variance: αβ2.
'Mathematics > Probability & Statistics' 카테고리의 다른 글
| 12. 표본평균(Sample Mean) (0) | 2024.07.06 |
|---|---|
| 11. 정규분포(Normal Distribution) (0) | 2024.07.06 |
| 09. 이산확률변수 - 2(Discrete Random Variable - 2) (0) | 2024.07.06 |
| 08. 이산확률변수 - 1(Discrete Random Variable - 1) (0) | 2024.07.06 |
| 07. 결합확률분포 기댓값(Expected Value of Joint Probability Distribution) (0) | 2024.07.06 |





