엔지니어가 되고 싶은 공돌이
12. 고유값과 고유벡터(Eigenvalue and Eigenvector) 본문

12. 1. 고유값과 고유벡터(Eigenvalue and Eigenvector)
- Ax = λx 를 만족하는 0이 아닌 벡터가 존재하면, Scalar λ를 A의 고유값(Eigenvalue)라 부르고, x를 λ에 대응하는 A의 고유벡터(Eigenvector)라 부른다.
- Eigenvector x는 선형변환을 해도 그 결과가 같은 벡터로, Eigenvalue에 따라 늘어나거나, 축소하거나, 방향만 변하고, 나머지 성질은 변하지 않는 벡터이다.
- 고유공간(EigenSpace): 영 벡터와 고유값 λ에 대응하는 모든 고유벡터의 집합.
1) 고유값 계산(Eigenvalue Calculation).
- 고유방정식(= 특성방정식, Characteristic Equation): det(A - λI) = 0.
- 고유방정식의 해가 Eigenvalue이다.
2) 고유벡터 계산(Eigenvector Calculation).
- (A - λiI)x = 0에 대응하는 벡터 x.

- 삼각행렬의 고유값은 주 대각선의 각 원소이다.
- Eigenvalue 에 0이 있으면 행렬 A는 가역행렬이 아니다.
12. 2. 특성방정식(Characteristic Equation)
- 대수적 중복도(Algebraic Multiplicity): Eigenvalue가 얼마나 많이 중복되었는지를 나타내는 값.
- 기하학적 중복도(Geometric Multiplicity): 각 Eigenvalue에 해당하는 Eigenvector가 이루고있는 고유공간의차원.
기하학적 중복도는 각 Eigenvalue마다 하나씩 존재하며, 대수적 중복도 보다 작거나 같다.
Geometric Multiplicity = 열의 개수 – rank(A - λI).
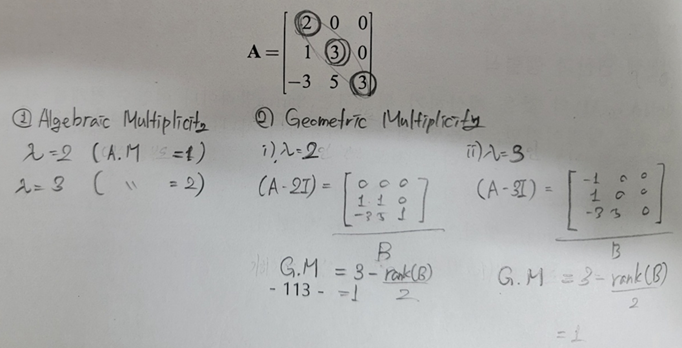
- n-square Matrix A, B에 대하여, P-1AP = B or PBP-1 = A 일 때, A와 B는 서로 닮은 행렬(Similar Matrix)이라 말한다. 그리고 A에서 B로 바꾸는 것을 닮은 변환(Similarity Transformation)이라 부른다.
- A와 B가 닮은 행렬(Similar Matrix)이면 A와 B는 같은 Characteristic Equation, Algebraic Multiplicity, Geometric Multiplicity, Eigenvalue를 갖는다. 하지만 Eigenvector는 같지 않을 수 있다.
'Mathematics > Linear Algebra' 카테고리의 다른 글
| 14. 내적, 직교, 직교집합(Inner Product, Orthogonal, Orthogonal Set) (0) | 2024.06.29 |
|---|---|
| 13. 대각화(Diagonalization) (0) | 2024.06.29 |
| 11. 선형변환의 기하학적 의미(Geometric Meaning of Linear Transformation) (0) | 2024.06.29 |
| 10. 선형변환(Linear Transformation) (0) | 2024.06.29 |
| 09. 기저, 차원, 계수(Basis, Dimension, Rank) (0) | 2024.06.29 |





