엔지니어가 되고 싶은 공돌이
09. 기저, 차원, 계수(Basis, Dimension, Rank) 본문

9. 1. 기저, 차원, 계수(Basis, Dimension, Rank)
- 기저(Basis): Vector Space 안의 n개의 벡터들의 집합 B = {b1, b2, … , bn}가 다음 2가지 조건을 만족하면 집합 B를 Vector Space의 기저(Basis)라고 부른다.
1) B = {b1, b2, … , bn} 는 선형독립이다.
2) V = Span{b1, b2, … , bn} 즉, V를 생성한다.
- 하나의 Vector Space에 기저가 될 수 있는 집합은 여러 개가 있을 수 있다. 그러나 기저를 이루는 집합들의 각 원소의 개수는 모두 같다.
- Basis가 되기 위한 필요충분조건은 determinant ≠ 0.
- 표준기저(Standard Basis): Standard Unit Vector로 구성된 집합.
- 기저의 집합에 포함된 하나의 벡터가 나머지 벡터의 선형결합으로 표현되면 기저의 집합에서 그 벡터를 제거해도 해당 집합은 벡터공간을 생성할 수 있다.
- 널공간의 기저(Basis of Null Space): Ax = 0 의 해를 구하고, 그 해를 매개 벡터의 형태로 표현한다.
- 열공간의 기저(Basis of Column Space): pivot columns이 열공간의 기저(Basis of Column Space)를 이룬다.
- 행공간의 기저(Basis of Row Space): 행렬을 Row Echelon Form Matrix의 형태로 바꿨을 때 0이 아닌 행들이 행공간의 기저(Basis of Row Space)가 된다.

- 차원(Dimension, dim(V)): Basis Vector의 개수.
- 영공간의 차원은 0으로 정의하고, 3차원 부분공간에는 0차원, 1차원, 2차원, 3차원의 부분공간이 있다.
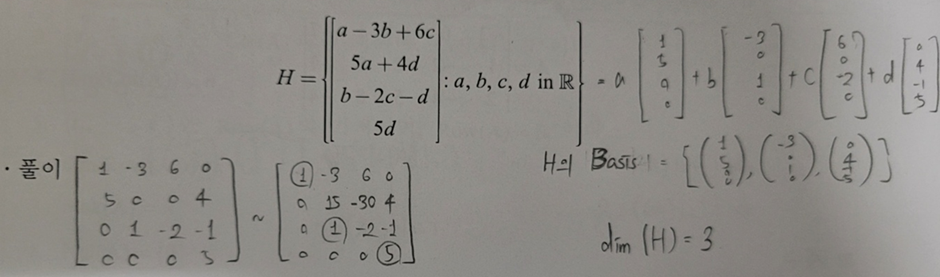
- 기저와 차원의 성질(Properties of Basis and Dimension)
1) Vector Space V(n Dimension)에서 m개의 벡터가 일차독립이면 m ≤ n이다. 따라서 m > n이면 m개의 벡터들은 일차종속이다.
2) Vector Space V(n Dimension)에서 n개의 벡터가 일차독립이면 n개의 벡터들은 Basis이다.
3) Vector Space V(n Dimension) = Span{v1, v2, … , vn} 이면 {v1, v2, … , vn}는 V의 기저이다.
- 차원의 성질(Properties of Dimension)
1) 0 ≤ dim(H) ≤ dim(V).
2) dim(H) = 0 <-> H = {0}.
3) dim(H) = dim(V) <-> H = V.
- dim(nul(A))은 Ax = 0의 Free Variable의 수와 같고, dim(Col(A)의 차원은 A의 pivot Column의 개수와 같다.
- 계수(Rank, rank(A)): Row Dimension of Matrix A or Column Dimension of Matrix A or 독립된 열벡터의 개수 or 독립된 행벡터의 개수.
- rank(A) = rank(AT).
- m x n Matrix A => rank(A) + dim(Nul(A)) = n.
9. 2. 좌표변환 행렬(Coordinate Transformation Matrix)
- B = {b1, b2, … , bn}가 Vector Space V의 Basis라 할 때, V 위의 임의의 벡터 x는 적당한 scalar c1, c2, … , cn으로 유일하게 표시된다.
x = c1b1 + c2b2 + … + cnbn.
- scalar c1, c2, … , cn을 x의 좌표(Coordinate of x)라 부르고 [x]B 라 부른다.
- 좌표를 표현하는 가장 기본적인 방법은 표준기저를 이용해서 표현하는 것이지만, 표준기저 외에 새로운 기저로도 표현이 가능하다. 즉, 동일한 벡터를 기저에 따라 다르게 표현하는 방법이다.
- 좌표변환 행렬(Coordinate Transformation Matrix, PB): Basis B에서 Standard Basis e로 좌표를 바꿔주는 행렬.
- 좌표사상(Coordinate Mapping, PB-1): Standard Basis e에서 Basis B로 바꿔주는 행렬.
'Mathematics > Linear Algebra' 카테고리의 다른 글
| 11. 선형변환의 기하학적 의미(Geometric Meaning of Linear Transformation) (0) | 2024.06.29 |
|---|---|
| 10. 선형변환(Linear Transformation) (0) | 2024.06.29 |
| 08. 벡터공간(Vector Space) (0) | 2024.06.29 |
| 07. 행렬식의 성질(Properties of Determinant) (0) | 2024.06.29 |
| 06. 행렬식(Determinant) (0) | 2024.06.29 |




