엔지니어가 되고 싶은 공돌이
10. 선형변환(Linear Transformation) 본문

10. 1. 선형변환과 행렬(Linear Transformation and Matrix)
- 입력과 출력이 모두 vector인 함수를 변환(Transformation)이라 부른다.
Rn (Domain)에서 Rm (Codomain)으로의 변환 T는 T: Rn -> Rm 로 표시한다.
- 선형변환(Linear Transformation): T: Rn -> Rm 이 임의의 vector u, v 와 임의의 scalar k에 대하여 다음 2조건을 만족하면 선형변환(Linear Transformation)이라 부른다.
1) T(u + v) = T(u) + T(v).
2) T(ku) = kT(u).

- 선형변환의 성질(Properties of Linear Transformation).
1) T(0) = 0.
2) T(k1v1 + k2v2 + … + knvn) = k1T(v1) + k2T(v2) + … + knT(vn).
- 영변환(Zero Transformation): T를 T(v) = 0으로 정의.
- 항등변환(Identity Transformation):T를 T(v) = v로 정의.
- 행렬변환(Matrix Transformation): T(x) = Ax.
1) 모든 Linear Transformation은 Matrix Transformation으로 나타낼 수 있다.
2) 모든 Matrix Transformation은 Linear Transformation이다.
3) T(x) = Ax를 만족하는 Matrix A는 유일하게 존재한다.
- 표준행렬(Standard Matrix): A = [T(e1), T(e2), … T(en)].
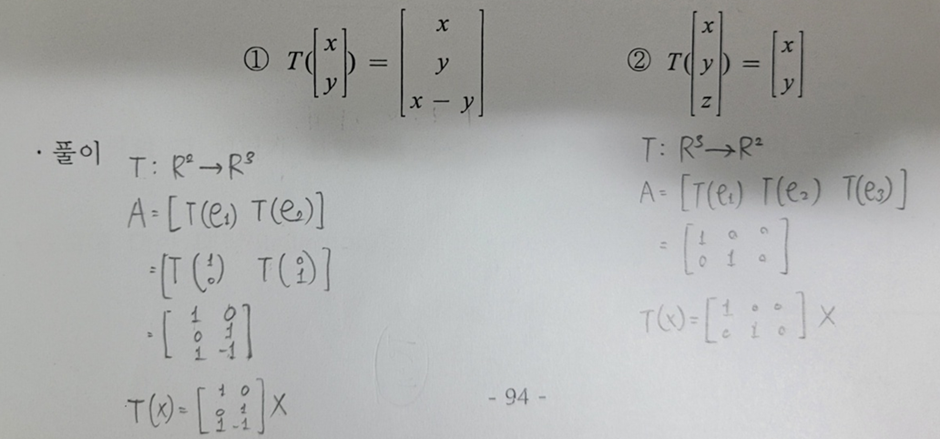
'Mathematics > Linear Algebra' 카테고리의 다른 글
| 12. 고유값과 고유벡터(Eigenvalue and Eigenvector) (0) | 2024.06.29 |
|---|---|
| 11. 선형변환의 기하학적 의미(Geometric Meaning of Linear Transformation) (0) | 2024.06.29 |
| 09. 기저, 차원, 계수(Basis, Dimension, Rank) (0) | 2024.06.29 |
| 08. 벡터공간(Vector Space) (0) | 2024.06.29 |
| 07. 행렬식의 성질(Properties of Determinant) (0) | 2024.06.29 |





