엔지니어가 되고 싶은 공돌이
08. 벡터공간(Vector Space) 본문

8. 1. 벡터공간, 부분공간(Vector Space, Sub Space)
- 벡터공간(Vector Space): 벡터를 원소로 가지는 공간에서 덧셈 연산과 스칼라 곱셈 연산의 공리가 만족되는 집합.
(First Axiom : Addition Operation). [u, v, w is vector and a, b is scalar]
1) u + v = v + u.
2) (u + v) + w = u + (v + w).
3) u + 0 = 0 + u = u.
4) u + (-u) = 0.
(Second Axiom : Scalar Multiplication Operation). [u, v, w is vector and a, b is scalar]
1) a(u + v) = au + av.
2) (a + b)u = au + bu.
3) a(bu) = (ab)u.
4) 1u = u.
- 벡터공간 내에서 임의의 벡터에 대한 역벡터와 벡터공간 전체에 대한 영벡터는 그 존재가 유일하다.
- 부분공간(Sub Space): Vector Space 내에 포함된 또 다른 Vector Space.
Sub Space H는 Vector Space V의 Zero Vector를 포함하고, Vector Space V의 덧셈 연산과 스칼라 곱셈 연산을 만족한다.
- Sub Space H = Span {v1, v2, … , vn} = Linear Combination = k1v1 + k2v2 + … + knvn.
Linear Combination으로 새로운 Sub Space을 생성할 수 있다.
8. 2. 널공간, 열공간, 행공간(Null Space, Column Space, Row Space)
- m X n Matrix A의 Null Space, Row Space는 Rn의 Sub Space 이고 Column Space는 Rm의 Sub Space이다.
- 널공간(Null Space, Nul(A)): Homogeneous System of Linear Equation의 해 집합.
- 널공간의 성질(Properties of Null Space).
1) Ax = 0 으로 구해진 해집합을 Span으로 표현할 때 Span 내부의 벡터들은 독립이다.
2) Nul(A)를 통해 생성되는 Span 내부의 벡터들은 Homogeneous System of Linear Equation의 Free Variable의 수와 같다.

- 열공간(Column Space Col(A)): A의 column vector들의 모든 선형결합의 집합.
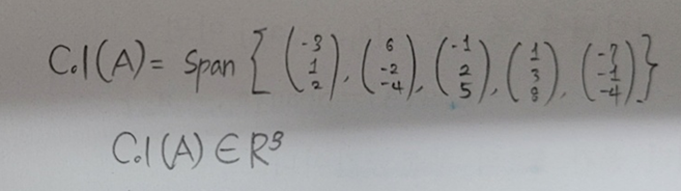
- 행공간(Row Space, Row(A)): A의 row vector들의 모든 선형결합의 집합.
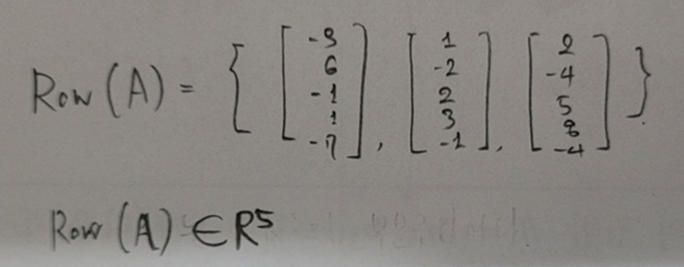
- 두 행렬 A와 B가 행동치(~) 이면 두 행렬의 Row Space는 같다.
- Row(A)와 Nul(A)는 영벡터를 공통적으로 가지고 있으며, 서로 수직관계이다.
'Mathematics > Linear Algebra' 카테고리의 다른 글
| 10. 선형변환(Linear Transformation) (0) | 2024.06.29 |
|---|---|
| 09. 기저, 차원, 계수(Basis, Dimension, Rank) (0) | 2024.06.29 |
| 07. 행렬식의 성질(Properties of Determinant) (0) | 2024.06.29 |
| 06. 행렬식(Determinant) (0) | 2024.06.29 |
| 05. 다양한 행렬(Various Matrix) (0) | 2024.06.27 |





