엔지니어가 되고 싶은 공돌이
11. 직선과 평면의 방정식(Equations of Straight Lines and Planes) 본문
11. 직선과 평면의 방정식(Equations of Straight Lines and Planes)
Geca 2024. 4. 15. 17:58
11. 1. 직선의 방정식(Equation of a Straight Line)

- position vector a 인 점 A를 지나고 vector u에 평행한 직선의 방정식
p = a + tu. [p is vector & t is real number]
- 점 A(x1 , y1, z1) 을 지나고 vector u = (a, b, c) 에 평행한 직선의 방정식
(x – x1) / a = (y – y1) / b = (z – z1) / c.
만약 분모가 0이면 ex) a = 0 이면, 방정식은 x = x1 , (y – y1) / b = (z – z1) / c 꼴로 표현한다.
- 두 점 A(x1 , y1 , z1), B(x2 , y2 , z2) 를 지나는 직선의 방정식
(x – x1) / (x2 – x1) = (y – y1) / (y2 – y1) = (z – z1) / (z2 – z1).
11. 2. 두 직선 각의 크기(Angle Between Two Lines)
- 두 직선 l1 , l2 의 vector가 각각 u1 = (a1 , b1 , c1), u2 = (a2 , b2 , c2) 일 때, 두 직선이 이루는 각의 크기를 θ[0 ≤ θ ≤ π/2] 라 하면
=> cos θ = | u1 · u2 | / | u1 | | u2 |.
- 두 직선 l1 , l2 의 vector가 각각 u1 = (a1 , b1 , c1), u2 = (a2 , b2 , c2) 일 때,
1) l1 ⊥ l2 <=> u1 · u2 = a1a2 + b1b2 + c1c2 = 0.
2) l1 // l2 <=> u1 · u2 = ± | u1 | | u2 |.
u1 = ku2 .
a1 / a2 = b1 / b2 = c1 / c2 .
11. 3. 평면의 방정식(Equations of Planes)
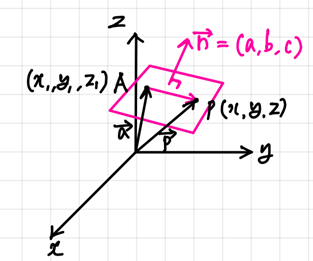
- 점 A(x1 , y1 , z1) 을 지나고 vector n = (a, b, c) 에 수직인 평면의 방정식
a(x – x1) + b(y – y1) + c(z – z1) = 0.
- 좌표공간에서 x, y, z에 관한 일차방정식 ax + by + cz + d = 0 은 벡터 n = (a, b, c)에 수직인 평면을 나타낸다.
- 두 평면의 교선의 방정식은 두 평면의 방정식을 연립하여 한 문자를 다른 두 문자에 대한 식으로 나타내여 구한다.
- 두 평면 ax + by + cz + d = 0, a’x + b’y + c’z + d’ 의 교선을 포함하는 평면의 방정식은
ax + by + cz + d + k(a’x + b’y + c’z + d’) = 0. [k is real number]
11. 4. 두 평면의 각의 크기(The Size of the Angle between Two Planes)
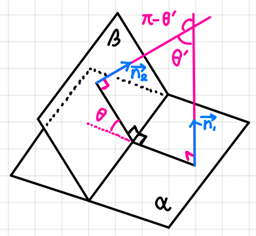
- 두 평면 A , B의 법선 벡터가 각각 n1 = (a1 , b1 , c1), n2 = (a2 , b2 , c2) 일 때, 두 평면이 이루는 각의 크기를 θ[0 ≤ θ ≤ π/2] 라 하면
=> cos θ = | n1 · n2 | / | n1 | | n2 |.
- 직선의 방향벡터를 u, 평면의 법선벡터를 n 이라 하면, 직선과 평면이 이루는 각의 크기 θ는
=> cos(π/2 - θ) = sinθ = | u · n | / | u | | n |.
- 두 평면 A, B 의 vector가 각각 n1 = (a1 , b1 , c1), n2 = (a2 , b2 , c2) 일 때,
1) A ⊥ B <=> n1 · n2 = a1a2 + b1b2 + c1c2 = 0.
2) A // B <=> n1 = kn2 .
a1 / a2 = b1 / b2 = c1 / c2 .
11. 5 점과 평면 사이의 거리(Distance Between Point and Plane)
- 점 A(x1 , y1 , z1) 와 평면 ax + by + cz + d = 0 사이의 거리는
| ax1 + by1 + cz1 + d| / √(a2 + b2 + c2).
'Basic Mathematics > High School_Geometry and Vector' 카테고리의 다른 글
| 10. 공간 벡터(Space Vector) (0) | 2024.04.14 |
|---|---|
| 09. 좌표공간(Coordinate Space) (0) | 2024.04.13 |
| 08. 공간 도형(Three-dimensional Figure) (0) | 2024.04.12 |
| 07. 평면 운동(Plane Motion) (0) | 2024.04.11 |
| 06. 평면벡터의 내적(Dot Product of Plane Vector) (0) | 2024.04.10 |