엔지니어가 되고 싶은 공돌이
08. 무리함수(Irrational function) 본문

8. 1. 무리식(Irrational expression)
- 무리식(Irrational expression): 유리식으로 나타낼 수 없고, root 안에 문자가 포함되어 있는 식.
- 실수라는 조건하에서 정의역의 범위: 분모 ≠ 0, (root 안의 식의 값) ≥ 0.
- 무리수가 서로 같을 조건
1) a + b√c = 0. ⇔ a = 0, b = 0.
2) a + b√c = d + e√c. ⇔ a = d, b = e.
3) a + √b = c + √d. ⇔ a = c, b = d.
유리수는 유리수끼리, 무리수는 무리수끼리 비교한다.
8. 2. 무리함수(Irrational function)
- 무리함수(Irrational function): y = f(x)에서 f(x)가 root를 포함할 때.
- 무리함수의 역함수를 그릴 때, 역함수의 정의역은 무리함수의 치역이다. 주의하자.
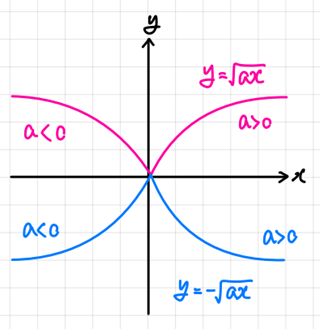
- y = ±√ax.
1) y = ±√ax 의 그래프는 | a | 의 값이 커질수록 x축에서 멀어진다.
2) 정의역은 a > 0이면 x ≥ 0 , a < 0이면 x ≤ 0.
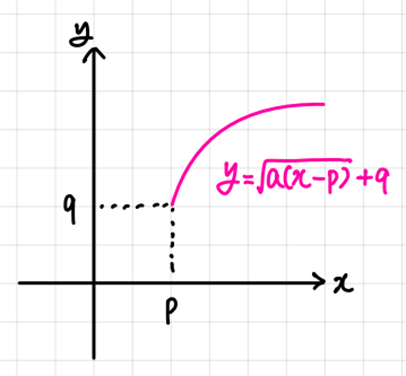
- y = √a(x - p) + q.
1) y = √ax의 그래프를 x축의 방향으로 p만큼, y축의 방향으로 q만큼 평행이동한 그래프.
2) 정의역은 a > 0이면 x ≥ p , a < 0이면 x ≤ p.
- y = √(ax + b) + c.
1) 이 그래프는 y = √a(x + b/a) + c 의 형태로 변형하여 그린다.
'Basic Mathematics > High School_Mathematics 2' 카테고리의 다른 글
| 10. 수열의 합 Σ, 수학적 귀납법(Sum of a sequence and Mathematical induction) (0) | 2024.03.09 |
|---|---|
| 09. 등차수열과 등비수열(Arithmetic sequence and Geometric sequence) (0) | 2024.03.09 |
| 07. 유리함수(Rational function) (0) | 2024.03.08 |
| 06. 함수(Function) - 2 (0) | 2024.03.07 |
| 05. 함수(Function) - 1 (1) | 2024.03.07 |
Comments





