엔지니어가 되고 싶은 공돌이
10. 수열의 합 Σ, 수학적 귀납법(Sum of a sequence and Mathematical induction) 본문
10. 수열의 합 Σ, 수학적 귀납법(Sum of a sequence and Mathematical induction)
Geca 2024. 3. 9. 15:37
10. 1 Σ의 기본공식(formula of sigma)
- 수열의 첫째항부터 제 n항 까지의 합을 기호로 Σ를 이용하여 간단히 나타낸다.

- Σ의 기본성질.

- 자연수와 거듭제곱의 합.

10. 2. 여러가지 수열의 합(Sum of various sequences)
- 분수꼴(Fraction)로 된 수열의 합은 부분분수로 변형하여 계산한다.
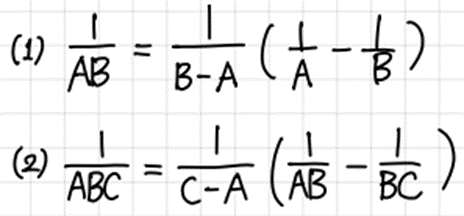
- 무리수(Irrational number)를 가지고 있는 수열의 합은 분모를 유리화 하고, 자연수를 차례로 대입하여 계산한다.
- 군수열: 수열에서 몇 개의 항이 일정한 규칙에 따라서 존재하며, 그에 따라 짝을 정할 수 있는 수열.
앞에서부터 규칙에 따라 분류하여 제 1 군, 제 2 군, 제 3 군, … 으로 부른다.
- 군수열을 푸는 방법은 앞에서부터 규칙성을 갖는 군으로 묶고, 각 군의 항의 개수랑 규칙을 찾은 뒤, 각 군의 일반항을 구한다.
10. 3. 수학적 귀납법 정의(Definition of mathematical induction)
- 귀납(Induction): 개개의 특징을 바탕으로 전체의 특징을 이끌어내는 과정.
- 수열의 귀납적 정의(Inductive definition of sequence): 수열을 첫째항과, 이웃하는 두 항의 관계식(일반적으로 an, an+1)으로 정의하는 방법.
- 등차수열의 귀납적 정의(Inductive definition of arithmetic sequence).
1) an+1 – an = d.
2) 2an+1 = an + an+2.
- 등비수열의 귀납적 정의(Inductive definition of geometric sequence).
1) an+1 / an = r.
2) an+12 = an X an+2.
'Basic Mathematics > High School_Mathematics 2' 카테고리의 다른 글
| 11. 지수, 로그(Exponent and Log) (0) | 2024.03.10 |
|---|---|
| 09. 등차수열과 등비수열(Arithmetic sequence and Geometric sequence) (0) | 2024.03.09 |
| 08. 무리함수(Irrational function) (0) | 2024.03.08 |
| 07. 유리함수(Rational function) (0) | 2024.03.08 |
| 06. 함수(Function) - 2 (0) | 2024.03.07 |




