엔지니어가 되고 싶은 공돌이
03. 복소수(Complex number) 본문

3. 1. 복소수(Complex number)
- 실수범위에서 제곱하여 음수가 되는 수는 없다.
- 제곱하여 -1 이 되는 수를 √-1 이라 하고, 문자 i로 표기하며, 허수단위(Imaginary unit)라고 부른다.
√-1 = i, -1 = i2.
√-a = √ai, (√ai)2 = -a.
- 복소수(Complex number)는 실수(Real number)와 허수(Imaginary number)를 포함하는 수체계이다.
복소수 표기방법: a + bi (a: 실수, b: 허수).
- b = 0일 때 실수가 되고, b ≠ 0일 때 허수가 되며 특히 허수 중에서 a = 0이면 순허수(pure imaginary number)라고 부른다.
- i는 제곱할 때 마다 i -> -1 -> -i -> 1 사이클로 순환한다.
- 복소수 z가 실수이면 z2 ≥ 0 조건이 성립되고, 복소수 z가 순허수이면 z2 < 0 조건이 성립된다.
3. 2. 켤레복소수(Conjugate complex number)
- 복소수 z = a + bi에 대하여 허수부분의 부호를 바꾼 a – bi를 z의 켤레복소수(Conjugate complex number)라 부른다.
- 켤레복소수의 성질 (Properties of conjugate complex number).
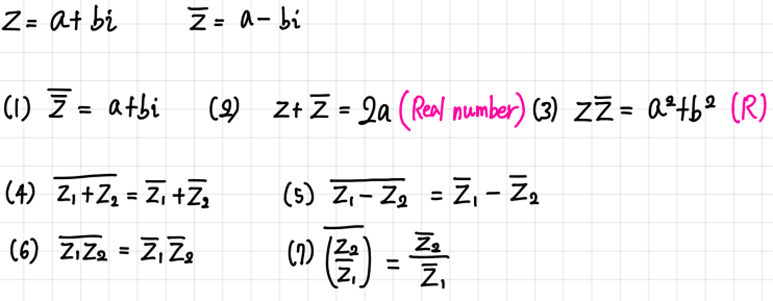
3. 3. 복소수의 사칙연산(Operations of complex number)
실수 a, b, c, d 에 대하여
1) 덧셈(Addition): (a + bi) + (c + di) = a + c + (b + d)i.
2) 뺄셈(Subtraction): (a + bi) - (c + di) = a – c + (b - d)i.
3) 곱셈(Multiplication): (a + bi)(c + di) = ac – bd + (ad + bc)i.
4) 나눗셈(Division): (a + bi) / (c + di) = (a + bi)(c - di) / (c + di)(c - di) = (ac + bd) / (c2 + d2) + (bc – ad)i / (c2 + d2).
나눗셈은 분모의 켤레복소수를 분모와 분자에 곱하여 분모를 실수화 해준다.
3. 4. 복소수가 서로 같을 조건(Equality of two complex number)
실수 a, b, c, d 에 대하여
1) a + bi = c + di 이면 a = c, b = d 이어야 한다(실수는 실수끼리, 허수는 허수끼리 비교한다).
2) a + bi = 0이면 a = b = 0이어야 한다.
'Basic Mathematics > High School_Mathematics 1' 카테고리의 다른 글
| 06. 이차함수와 이차방정식(Quadratic functions and quadratic equations) - 2 / 07. 다양한 방정식(Various equations) - 1 (1) | 2024.02.26 |
|---|---|
| 05. 이차함수와 이차방정식(Quadratic functions and quadratic equations) - 1 (1) | 2024.02.25 |
| 04. 방정식(Equation) (0) | 2024.02.24 |
| 02. 다항식(Polynomial) - 2 (0) | 2024.02.22 |
| 01. 다항식(Polynomial) - 1 (0) | 2024.02.20 |




