엔지니어가 되고 싶은 공돌이
02. 다항식(Polynomial) - 2 본문

2. 1. 항등식(Identity)
- 항등식(Identity)에서 양변의 동류항의 계수는 같다.
1) ax2 + bx + c = 0이 x에 대한 항등식이면 a = 0, b = 0, c = 0 이다.
2) ax2 + bx + c = dx2 + ex + f이 x에 대한 항등식이면 a = d, b = e, c = f 이다.
- 항등식의 성질을 만족하는 식에서, 알 수 없는 미지수가 있다면 변수에 임의의 수치를 대입하거나 동류항끼리 계수를 비교해서 미지수를 결정할 수 있다.
2. 2. 나머지정리와 인수정리(Remainder theorem and factor theorem)
- 나머지 정리(Remainder theorem).
x에 대한 다항식 f(x)에 대하여
f(x)를 x – a로 나눈 나머지를 R이라고 하면 R = f(a)가 성립.
f(x)를 ax – b로 나눈 나머지를 R이라고 하면 R = f(b/a)가 성립.
- 인수 정리(Factor theorem).
x에 대한 다항식 f(x)에 대하여
f(x)가 x – a로 나누어 떨어진다면 R = f(a) = 0이 성립.
- 조립제법과 나머지정리는 나누는 식이 x – a 즉, 일차식일 경우에만 이용한다.
2. 3. 인수분해(Factorization)
- 인수분해는 전개의 역과정이다.
1) 곱셈공식의 역과정이 인수분해의 공식이다.
2) 공통부분이 있다면 공통부분을 치환해서 인수분해한다.
3) x4 + ax2 + b의 꼴의 4차식은 x2을 문자로 치환하거나, A2 - B2의 꼴로 변형하여 인수분해한다.
4) 여러문자를 가지고 있는 다항식이면 차수가 가장 낮은 한 문자에 대하여 정리하고 인수분해한다.
5) 인수정리를 이용하여 인수분해를 수행할 수 도 있다.
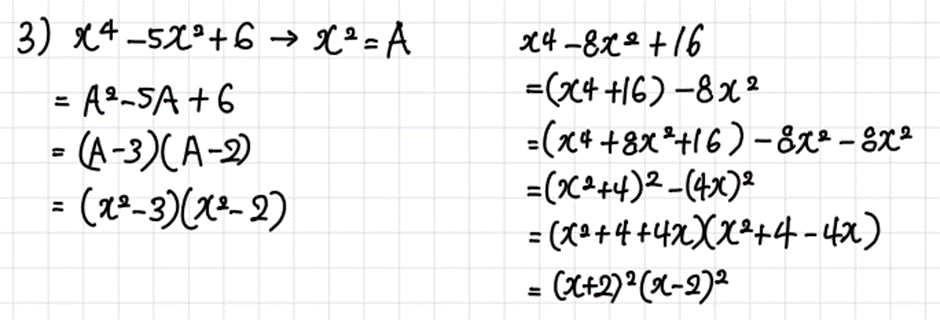
'Basic Mathematics > High School_Mathematics 1' 카테고리의 다른 글
| 06. 이차함수와 이차방정식(Quadratic functions and quadratic equations) - 2 / 07. 다양한 방정식(Various equations) - 1 (1) | 2024.02.26 |
|---|---|
| 05. 이차함수와 이차방정식(Quadratic functions and quadratic equations) - 1 (1) | 2024.02.25 |
| 04. 방정식(Equation) (0) | 2024.02.24 |
| 03. 복소수(Complex number) (0) | 2024.02.23 |
| 01. 다항식(Polynomial) - 1 (0) | 2024.02.20 |





