엔지니어가 되고 싶은 공돌이
14. 도형의 성질(Properties of shapes) / 15. 도형의 닮음(Similarity) 본문
14. 도형의 성질(Properties of shapes) / 15. 도형의 닮음(Similarity)
Geca 2024. 2. 17. 16:51
14. 1. 삼각형의 성질(Properties of triangle)
- 이등변삼각형(Isosceles triangle): 두 변의 길이가 같은 삼각형.
이등변삼각형의 성질: 두 밑각의 크기는 같다. / 꼭지각의 이등분선은 밑변을 수직 이등분한다.
이등변삼각형이 되는 조건: 두 내각의 크기가 같은 삼각형은 이등변삼각형이다.
- 직각삼각형의 합동조건(Right triangle congruence theorem).
1) RHA 합동(RHA Congruence): 두 직각삼각형의 빗변의 길이와 한 예각의 크기가 각각 같을 때.
2) RHS 합동(RHS Congruence): 두 직각삼각형의 빗변의 길이와 다른 한변의 길이가 각각 같을 때.
- 삼각형의 외심(Circumcenter): 삼각형의 세 변의 수직이등분선은 한 점에서 만나고, 이 점(외심)에서 삼각형의 세 꼭짓점에 이르는 거리는 모두 같다.
- 삼각형의 내심(Incenter): 삼각형의 세 내각의 이등분 선은 한 점에서 만나고, 이 점(내심)에서 삼각형의 세변에 이르는 거리는 모두 같다.
14. 2. 사각형의 성질(Properties of square)
- 평행사변형(Parallelogram)의 정의: 두 쌍의 대변이 각각 평행한 사각형.
평행사변형의 성질: 두 쌍의 대변의 길이는 각각 같다. / 두 쌍의 대각의 크기는 각각 같다. /
두 대각선은 서로 다른 것을 이등분 한다.

- 평행사변형이 되는 조건(Conditions for parallelograms).
1) 두 쌍의 대변이 각각 평행하다.
2) 두 쌍의 대변의 길이가 각각 같다.
3) 두 쌍의 대각의 크기가 각각 같다.
4) 한 쌍의 대변이 평행하고, 그 길이가 같다.
5) 두 대각선이 서로 다른 것을 이등분한다.
- 직사각형(Rectangle) 정의: 네 각의 크기가 모두 같은 사각형.
직사각형 성질: 두 대각선의 길이가 서로 같고, 서로 다른 것을 이등분한다.
- 마름모(Rhombus) 정의: 네 변의 길이가 모두 같은 사각형.
마름모 성질: 두 대각선은 서로 다른 것을 수직 이등분한다.
- 정사각형(Square) 정의: 네 변의 길이가 모두 같고, 네 각의 크기가 모두 같은 사각형.
정사각형 성질: 두 대각선의 길이가 서로 같고, 서로 다른 것을 수직이등분한다.
- 사다리꼴(Trapezoid) 정의: 한쌍의 대변이 평행한 사각형.
- 등변사다리꼴(Isosceles trapezoid) 정의: 밑변의 양 끝각의 크기가 같은 사다리꼴.
등변사다리꼴 성질: 평행하지 않은 한 쌍의 대변의 길이가 같고, 두 대각선의 길이가 같다.
- 정사각형 ⊂ 직사각형 ⊂ 평행사변형 ⊂ 사다리꼴 ⊂ 사각형.
⊂ 마름모 ⊂
15. 1. 도형의 닮음(Similarity)
- 평면도형에서의 닮음은 대응하는 변의 길이의 비가 일정하고, 대응하는 각의 크기는 각각 같다.
- 입체도형에서의 닮음은 대응하는 모서리의 길이의 비가 일정하고, 대응하는 면은 닮은 도형이다.
- 삼각형의 닮음조건(Similar conditions of triangle).
1) 세 쌍의 대응하는 변의 길이의 비가 각각 같다. (SSS 닮음(Similarity)).
2) 두 쌍의 대응하는 변의 길이의 비가 각각 같고, 그 끼인각의 크기가 같다. (SAS 닮음(Similarity)).
3) 두 쌍의 대응하는 각의 크기가 각각 같다. (AA 닮음(Similarity)).
15. 2. 닮음의 활용(Use of similarity)
- 평행선과 선분의 길이의 비(The ratio of the length of the line segments between parallel lines ).
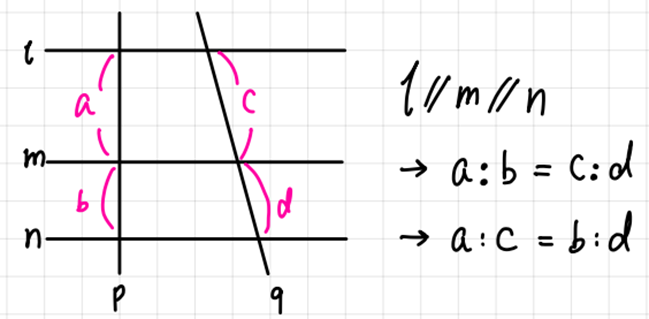
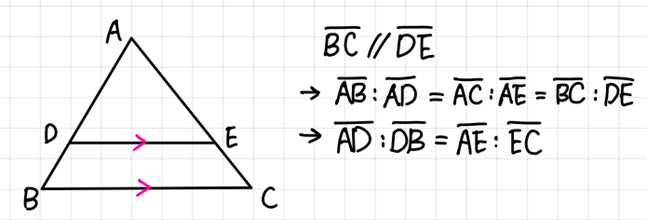
- 삼각형의 중점 연결 정리(Double point theorem of triangle).
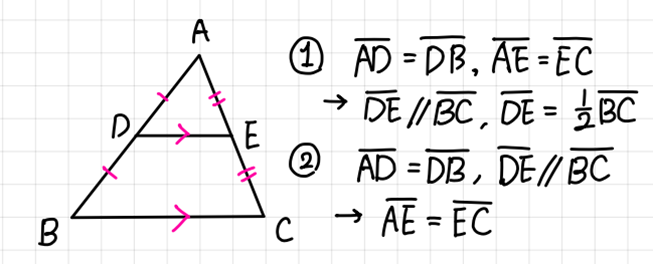
- 삼각형의 무게중심(Centroid of triangle).
중선(Median line): 삼각형에서 한 꼭짓점과 그 대변의 중점을 이은 선분.
삼각형의 무게중심(Centroid): 삼각형의 세 중선의 교점.
삼각형의 무게중심은 세 중선의 길이를 각 꼭짓점으로부터 2:1로 나눈다.
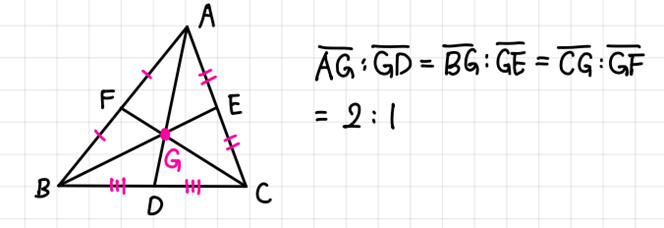
- 닮은 도형의 넓이와 부피(Area and volume of similar shapes).
닮음비가 m : n이면 넓이의 비는 m2 : n2이다.
닮음비가 m : n이면 부피의 비는 m3 : n3이다.
'Basic Mathematics > Middle School' 카테고리의 다른 글
| 19. 이차함수(Quadratic function) / 20. 통계-2(Statistics-2) (0) | 2024.02.19 |
|---|---|
| 16. 실수(Real number) / 17. 인수분해(Factorization) / 18. 이차방정식(Quadratic equation) (1) | 2024.02.18 |
| 12. 일차함수(Linear function) / 13. 확률(Probability) (0) | 2024.02.17 |
| 10. 식의 계산(Calculation of expressions) / 11. 방정식과 부등식(Equation and inequality) (0) | 2024.02.16 |
| 09. 유리수와 근삿값(Rational number and approximate value) (0) | 2024.02.16 |





