엔지니어가 되고 싶은 공돌이
07. 평면도형(Flane figure) / 08. 입체도형(Solid figure) 본문
07. 평면도형(Flane figure) / 08. 입체도형(Solid figure)
Geca 2024. 2. 15. 21:15
7. 1. 다각형(Polygon)
- 다각형(Polygon): 여러 개의 선분으로 둘러싸인 평면도형.
- 내각(Interior angle): 다각형에서 각 꼭짓점의 내부에 만들어진 각.
- 외각(Exterior angle): 각 꼭짓점에서 한 변의 연장선과 이웃하는 다른 변이 이루는 각.
- 대각선(Diagonal): 다각형에서 이웃하지 않는 두 꼭짓점을 이은 선분.
n각형의 한 꼭짓점에서 그을 수 있는 대각선의 개수는 (n-3)개이다.
n각형의 대각선의 총 개수는 n(n-3)/2개이다.
- n각형의 내각의 크기의 합은 180° X (n-2)이다.
- n각형의 외각의 크기의 합은 360°이다.
7. 2. 원(Circle)
- 원(Circle): 한 점 O로부터 일정한 거리에 있는 점의 집합.
- 호AB(Arc): 원 위의 두 점 A, B를 양 끝점으로 하는 원의 일부분.
- 부채꼴(Circualr sector): 원 O에서 두 반지름 OA, OB와 호 AB로 이루어진 도형.
- 활꼴(Circualr segment): 현 CD와 호 CD로 이루어진 도형.

- 원에서 같은 크기의 중심각에 대한 호와 현의 길이는 각각 같다.
- 부채꼴의 호의 길이, 부채꼴의 넓이는 중심각의 크기에 정비례한다.
- 현의 길이는 중심각의 크기에 정비례하지 않는다.
7. 3. 원의 길이와 넓이(Circumference and area of a circle)
- 원주율(π, pi): 원의 둘레의 길이 / 원의 지름의 길이 = 3.14159….
- 원의 둘레의 길이(원주, Circumference) = 2πr.
- 원의 넓이(area of a circle) = πr2.
- 부채꼴의 원주: 2πr X (x / 360°), 부채꼴의 넓이: πr2 X (x / 360°). = 1/2rl [r: 원의 반지름, l: 호의 길이].
7. 4. 원의 위치 관계(Positional relationship of circles)
- 원과 직선사이의 위치 관계: 두 점에서 만난다. / 한 점에서 만난다. / 만나지 않는다.
- 두 원사이의 위치 관계: 서로 외부에 있다. / 외부에서 접한다. / 두 점에서 만난다. / 내부에서 접한다. /
한 원이 다른 원 안에 있다. / 두 원의 중심이 일치한다.
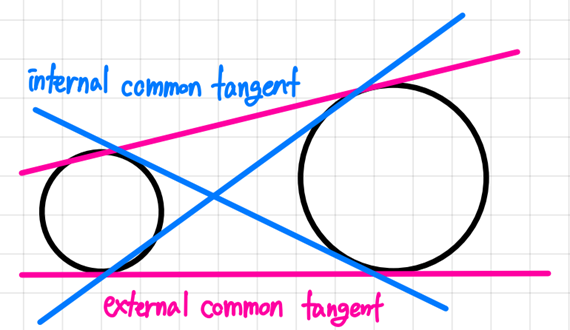
- 공통접선(Common tangent): 두 원에 동시에 접하는 접선.
두 원이 공통접선의 같은 쪽에 있으면 공통 외접선(External common tangent), 두 원이 다른 쪽에 있으면 공통 내접선(Internal common tangent)이라고 한다.
8. 1. 다면체
- 다면체(Polyhedron): 다각형으로 둘러싸인 입체도형.
다면체는 면의 개수에 따라 사면체, 오면체, 육면체… 라고 부른다.
다면체의 종류로는 n각기둥, n각뿔, n각뿔대가 있다.
- 정다면체(Regular polyhedron): 각 면이 모두 합동인 정다각형이고, 각 꼭지점에 모인 면의 개수가 모두 같은 다면체.
정사면체, 정육면체, 정팔면체, 정십이면체, 정이십면체.
| n각기둥 | n각뿔 | n각뿔대 | |
| 면의 개수 | n + 2 | n + 1 | n + 2 |
| 모서리의 개수 | 3n | 2n | 3n |
| 꼭짓점의 개수 | 2n | n + 1 | 2n |
8. 2. 회전체(Body of Rotation)
- 회전체(Body of Rotation): 평면도형을 한 직선을 축으로 하여 1회전 시켰을 때 생기는 도형.
- 회전체의 종류: 원기둥, 원뿔, 원뿔대, 구(Sphere, 구는 전개도가 없다).
- 회전체를 회전축에 수직인 평면으로 자른 단면은 항상 원이다.
- 회전체를 회전축을 포함하는 평면으로 자른 단면은 모두 합동이다.
8. 3. 입체도형의 겉넓이와 부피(Surface area and volume of solid figure)
1) 기둥의 겉넓이와 부피(triangular prism, Cylinder).
- 각기둥 겉넓이= 밑넓이 X 2 + 옆넓이. / 원기둥 겉넓이 = 2 πr2 + 2πrh.
- 각기둥 부피 = 밑넓이 X 높이. / 원기둥 부피 = πr2h.
2) 뿔의 겉넓이와 부피(Pyramid, Cone).
- 각뿔 겉넓이 = 밑넓이 + 옆넓이. / 원뿔 겉넓이 = πr2 + πrl[모선의 길이].
- 각뿔 부피 = 1/3 X 밑넓이 X 높이. / 원뿔 부피 = 1/3 πr2h.
3) 구의 겉넓이와 부피(Sphere).
- 구의 겉넓이 = 4 πr2. / 구의 부피 = 4/3 πr3.
'Basic Mathematics > Middle School' 카테고리의 다른 글
| 10. 식의 계산(Calculation of expressions) / 11. 방정식과 부등식(Equation and inequality) (0) | 2024.02.16 |
|---|---|
| 09. 유리수와 근삿값(Rational number and approximate value) (0) | 2024.02.16 |
| 05. 통계(Statistics) / 06. 도형의 기초(Basic of Shape) (0) | 2024.02.15 |
| 03. 문자와 식(Character and expression) / 04. 함수와 그래프(Function and graph) (1) | 2024.02.14 |
| 02. 정수와 유리수(Integer and rational number) (0) | 2024.02.14 |





