엔지니어가 되고 싶은 공돌이
03. 문자와 식(Character and expression) / 04. 함수와 그래프(Function and graph) 본문
03. 문자와 식(Character and expression) / 04. 함수와 그래프(Function and graph)
Geca 2024. 2. 14. 19:30
3. 1. 문자와 일차식(Character and linear equation)
- 문자를 사용하면 수량과 수량 사이의 관계를 식으로 간단히 나타낼 수 있다.
- 항(Term): 수 또는 문자의 곱으로 이루어진 식.
- 상수항(Constant term): 수만으로 된 항.
- 계수(Coefficient): 수와 문자의 곱으로 되어 있는 항에서 문자 앞에 곱해진 수.
- 다항식(Polynomial): 하나 이상의 항의 합으로 이루어진 식.
- 단항식(Monomial): 하나의 항으로 이루어진 다항식.
- 차수(Degree): 어떤 항에서 문자가 곱해진 개수.
- 일차식(Linear equation): 차수가 1인 다항식.
- 동류항(Similar terms): 문자와 차수가 같은 항. 그러므로 모든 상수항은 동류항이다.
3. 2. 일차방정식(Linear equation)
- 등식(equality): 등호 ‘ = ’를 이용하여, 두 수 또는 식이 같음을 나타내는 식.
- 방정식(equation): 미지수의 값에 따라 참이 되기도 하고, 거짓이 되기도 하는 등식.
- 항등식(Identity): 미지수가 어떤 값을 갖더라도 항상 참이 되는 등식.
- 등식의 성질(Properites of equation): 등식의 양변에 같은 수를 더하고, 빼고, 곱하고, 나누어도 등식은 성립한다.
4. 1. 함수의 정의(Definition of function)
- 변수(Variable): x, y 처럼 여러 가지로 변하는 값을 나타내는 문자.
- 상수(constant): 일정한 값을 가지는 수나 문자.
- 함수(function): x의 값이 변함에 따라 y의 값이 하나로 정해지는 대응 관계가 있을 때는 y는 x의 함수라 하고, 이 함수를 f라고 할 때 기호로 y = f(x)로 표현한다.
- 정의역(Domain): y = f(x)에서 변수 x가 속하는 집합.
- 공역(Codomain): y = f(x)에서 변수 y가 속하는 집합.
- 함숫값(Value of function): y의 값.
- 치역(Range): 함숫값 전체의 집합. 치역은 공역의 부분집합이다.
4. 2. 함수의 그래프(Graph of function)
- 순서쌍(Ordered pair): 위치를 나타내는 두 수의 순서를 생각하여 쌍으로 나타낸 것. (x, y)
- 좌표축(Coordinate axis): 두 수직선이 각각의 원점에서 수직으로 만날 때, 가로의 수직선을 x축, 세로의 수직선을 y축이라고 부른다. x축과, y축을 통틀어 좌표축이라고 부른다.
- 좌표평면(Coordinate plane): 좌표축이 정해져있는 평면.
- 원점(Origin): 두 좌표축이 만나는 점 O, 좌표로 (0, 0).


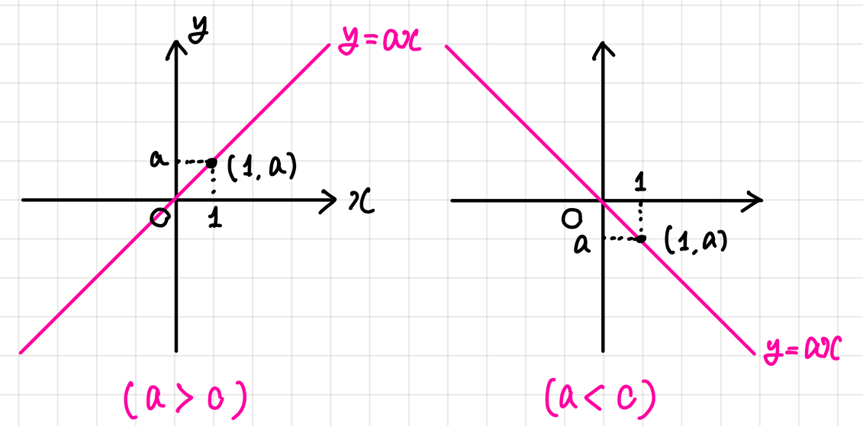

'Basic Mathematics > Middle School' 카테고리의 다른 글
| 09. 유리수와 근삿값(Rational number and approximate value) (0) | 2024.02.16 |
|---|---|
| 07. 평면도형(Flane figure) / 08. 입체도형(Solid figure) (0) | 2024.02.15 |
| 05. 통계(Statistics) / 06. 도형의 기초(Basic of Shape) (0) | 2024.02.15 |
| 02. 정수와 유리수(Integer and rational number) (0) | 2024.02.14 |
| 01. 집합과 자연수(Set and natural number) (0) | 2024.02.14 |





