엔지니어가 되고 싶은 공돌이
09. 부정적분과 정적분(Indefinite Integral and Definite Integral) 본문
Mathematics/Calculus
09. 부정적분과 정적분(Indefinite Integral and Definite Integral)
Geca 2024. 7. 16. 19:26
9. 1. 부정적분(Indefinite Integral)
- 적분은 미분의 역연산이다.
- F(x)의 도함수가 f(x) 일 때, F(x)를 f(x)의 부정적분(Indefinite Integral)이라 부른다.
- 적분의 기호로 ∫ (integral) 을 사용한다.
- ∫ f(x)dx = F(x) + C.
여기서 dx는 x를 기준으로 적분한다는 걸 의미하고, x를 적분변수(Integral Variable), C는 적분상수(Integral Constant)라 부른다.
9. 2. 정적분(Definite Integral)
- 부정적분은 함수(Function)를, 정적분은 실수(Real Number)(도형의 넓이와 부피 등)를 의미한다.
- 함수 f(x)가 구간 [a, b]에서 연속일 때,
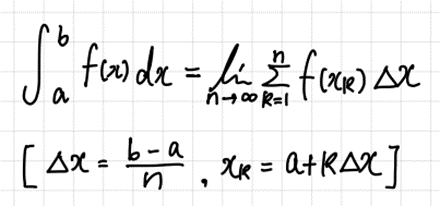
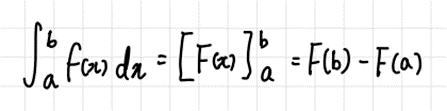
- 정적분의 성질(Properties of Definite Integral).
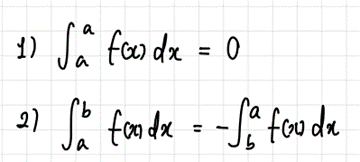
9. 3. 적분과 미분의 관계(Relationship between Integral and Differential)
- 함수 f(x)가 닫힌 구간 [a, b]에서 연속이고 a ≤ x ≤ b 일 때,

- 적분에 대한 평균값 정리(Mean Value Theorem for Integrals)
f가 [a, b]에서 연속이면, 다음을 만족하는 c가 [a, b]에 존재한다.
f(c) = 1/(b - a) ) ∫ab f(x) dx.
-> ∫ab f(x) dx = f(c)(b - a).
'Mathematics > Calculus' 카테고리의 다른 글
| 11. 적분의 활용(Use of Integral) (0) | 2024.07.17 |
|---|---|
| 10. 부정적분, 정적분의 계산(Calculation of indefinite Integrals and Definite Integrals) (0) | 2024.07.17 |
| 08. 미분의 활용(Use of Differentiation) (0) | 2024.07.16 |
| 07. 역삼각함수, 쌍곡선함수, 로피탈의 법칙(Inverse Trigonometric Function, Hyperbolic Function, L’Hospital’s Rule) (0) | 2024.07.16 |
| 06. 역함수의 도함수(Derivative of Inverse Function) (0) | 2024.07.15 |
Comments





