07. 역삼각함수, 쌍곡선함수, 로피탈의 법칙(Inverse Trigonometric Function, Hyperbolic Function, L’Hospital’s Rule)

 

7. 1. 역삼각함수(Inverse Trigonometric Function)

 

- 삼각함수는 일대일이 아니므로 역함수가 존재하지 않지만, 정의역을 축소시켜서 일대일로 만들어 역함수를 구할 수 있다.

 

- sin^-1 x = arcsin x. [-π/2 ≤ x ≤ π/2]

 

- cos^-1 x = arccos x. [0 ≤ x ≤ π]

 

- tan^-1 x = arctan x. [-π/2 < x < π/2]

 

 

- 역삼각함수의 미분(Differentiation of Inverse Trigonometric Function)

 

 

---

 

7. 2. 쌍곡선함수(Hyperbolic Function)

 

- 두 지수함수 e^x와 e^-x 의 특정한 결합은 널리 활용된다.

 

  1) sinh x (Hyperbolic sine) = (e^x – e^-x) / 2.

 

  2) cosh x (Hyperbolic cosine) = (e^x + e^-x) / 2.

 

  3) tanh x = sinh x / cosh x.

 

  4) csch x = 1 / sinh x.

 

  5) sech x = 1 / cosh x.

 

  6) coth x = cosh x / sinh x.

 

- 쌍곡선함수의 미분(Differentiation of Hyperbolic Function)

 

 

 

- 역쌍곡선함수(Inverse Hyperbolic Function)

 

 

 

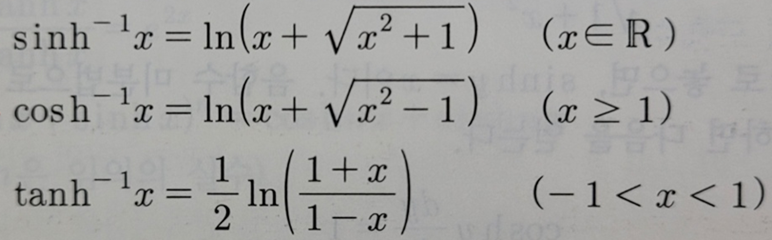
- 역쌍곡선함수의 미분(Differentiation of Inverse Hyperbolic Function)

 

 

---

 

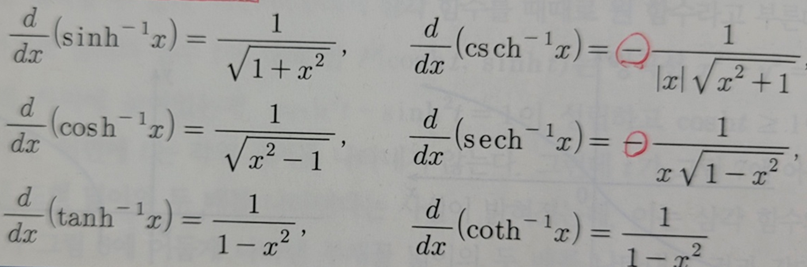
7. 3. 로피탈의 법칙(L’Hospital’s Rule)

 

- Definition: 0/0 꼴, ∞/∞ 꼴의 부정형이 있으면 lim (x → a) f(x)/g(x) = lim (x → a) f’(x)/g’(x).

 

- 0 X ∞ 꼴이면 fg = f / (1 / g) = g / (1 / f) 형태로 바꿔서 L’Hospital’s Rule을 적용한다.

 

---