05. 지수함수와 로그함수(Exponential Function and Logarithmic Function)

 

5. 1. 지수함수(Exponential Function)

- y = a^x (a > 0, a ≠ 1).

 

 

a > 1

 

 

0 < a < 1

 

 

- 지수함수 그래프의 성질(Properties of Exponential Function Graphs).

 

 1) 정의역(Domain)은 실수 전체의 집합이고, 치역(Codomain)은 양의 실수 전체의 집합이다.

 

 2) 그래프는 (0, 1), (1, a)를 지나고, x축이 점근선(Asymptote)이다.

 

 3) y = a^x 그래프와 y = (1/a)^x 그래프는 y축에 대하여 대칭이다.

 

 

- y = a^x 그래프를 x축으로 p, y축으로 q만큼 평행이동 -> y = a^(x-p) + q.

 

- y = a^x 그래프를 x축 대칭이면 y = -a^x , y축 대칭이면 y = a^-x , 원점 대칭이면 y = -a^-x .

 

---

 

5. 2. 로그함수(Logarithmic Function)

 

- y = log_a x (a > 0, a ≠ 1, x > 0).

 

- y = a^x 의 역함수이다.

 

 

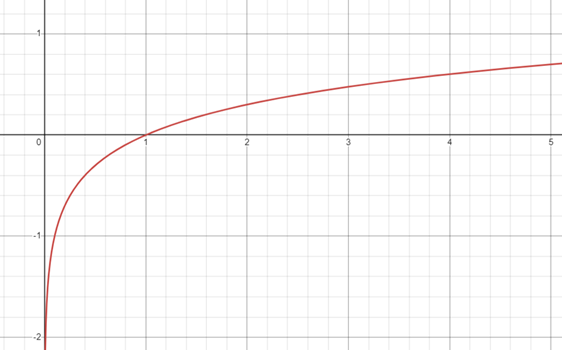
a > 1

 

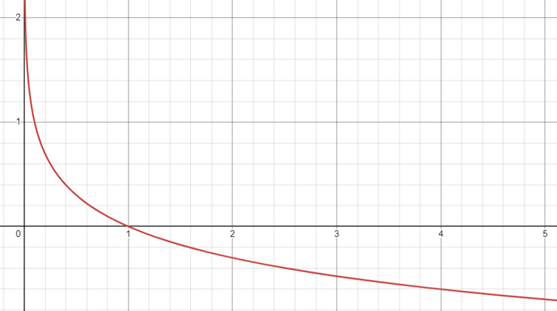
0 < a < 1

 

 

- 로그함수 그래프의 성질(Properties of Logarithmic Function Graphs).

 

 1) 정의역(Domain)은 양의 실수 전체의 집합이고, 치역(Codomain)은 실수 전체의 집합이다.

 

 2) 그래프는 (1, 0), (a, 1)를 지나고, y축이 점근선(Asymptote)이다.

 

 3) y = log_1/a x 그래프와 y = log_a x 그래프는 x축에 대하여 대칭이다.

 

 

- y = log_a x 그래프를 x 축으로 p만큼, y축으로 q만큼 평행이동 -> y = log_a (x – p) + q.

 

 정의역은 x > p 이고, 점근선의 방정식은 x = p 이다.

 

- y = log_a x 그래프를 x축 대칭이동 하면 y = log_a (1/x) , y축 대칭이동하면 y = log_a (-x) , 원점 대칭이동하면 y = log_a (-1/x) .

 

---

[1] https://www.desmos.com/calculator/