엔지니어가 되고 싶은 공돌이
14. 리차드슨 외삽법, 수치적분(Richardson Extrapolation and Numerical Integration) 본문
Mathematics/Numerical Analysis
14. 리차드슨 외삽법, 수치적분(Richardson Extrapolation and Numerical Integration)
Geca 2024. 7. 12. 14:17
14. 1. 리차드슨 외삽법(Richardson Extrapolation)
- Richardson Extrapolation: f’(x)의 오차를 O(h2)[Central Diffenence Formula]에서 O(h4)로 향상 시켜서 수렴속도를 가속화 시키는 방법이다.



14. 2. 수치적분(Numerical Integration)
- 수치적분법은 정적분을 대수적으로 구하기 어려울 때 사용한다.

- f(x)는 넓이를 구하고자 하는 함수이고, w(x)(w(x) > 0)는 가중치함수(Weighting Function)이다.
- 구간 [a, b]를 n+1등분하여 Integral의 근사값을 구하면 다음과 같다.
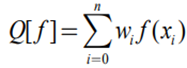
- 위 방법을 수치적분이라 부른다. 여기서 xi는 마디점(node), wi(weight)라 부른다.
- E[f](error) = I[f] – Q[f].
- 수치적분법은 마디점을 선택하는 방법에 따라 다르다.
- 마디점을 균등하게 나누는 방법을 뉴턴-코드 수치적분법(Newton-Cotes Numerical Integration)이라 부르고, [a, b]를 n으로 균등하게 나누면 h = (b – a) / n 로 정의 할 수 있다.
1) n = 1, T(f) (Trapezoid)
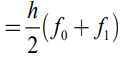
2) n = 2, S(f) (Simpson)
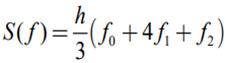
3) n = 3, S3(f)
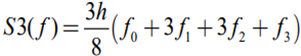
4) n = 4, B(f) (Boole)
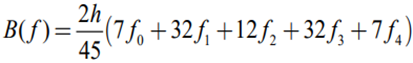
-> n이 커지면 커질수록 정확도는 높아진다.
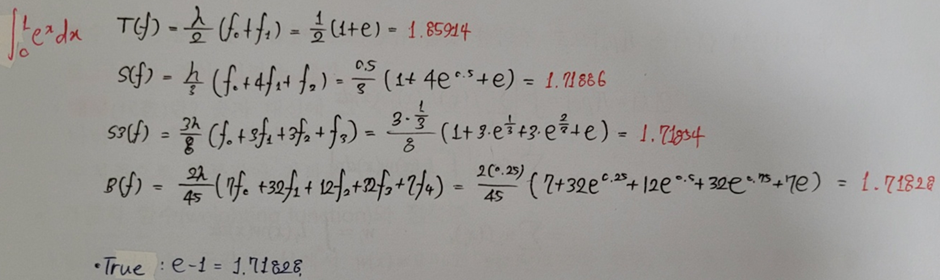
'Mathematics > Numerical Analysis' 카테고리의 다른 글
| 13. 테일러 수치미분법(Talyor’s Numerical Differentiation) (2) | 2024.07.12 |
|---|---|
| 12. 스플라인 함수(Spline Function) (1) | 2024.07.12 |
| 11. 뉴턴의 분할차분법(Newton’s Interpolator Divided Difference Formula) (0) | 2024.07.12 |
| 10. 라그랑주 보간법(Lagrange Interpolation) (0) | 2024.07.12 |
| 09. 비선형방정식 -2 (Non-Linear Equation - 2) (2) | 2024.07.12 |




