엔지니어가 되고 싶은 공돌이
02. 조건부확률(Conditional Probability) 본문

2. 1. 조건부확률(Conditional Probability)
- 조건부 확률(Conditional Probability, P(B | A)):사건 A가 일어났다는 전제 하에 사건 B가 일어날 확률.
- P(B | A) = n(A ∩ B) / n(A) = P(A ∩ B) / P(A).
- 조건부확률의 성질(Properties of Conditional Probability).
1) P(A U B | C) = P(A | C) + P(B | C) – P(A ∩ B | C).
2) P(AC | B) = 1 – P(A | B).
- 곱의 법칙(Multilplication Law): P(A1 ∩ … ∩ An) = P(A1)P(A2|A1)P(A3|A1∩A2)…P(An|A1∩ … ∩An-1).
- P(A ∩ B) = P(A)P(B | A).
- 독립(Independent): P(B) = P(B | A) or P(A) = P(A | B).
사건 A의 발생유무가 사건 B의 conditional probability에 아무런 영향을 미치지 못함.
- 종속(Dependent): P(B) ≠ P(B | A) or P(A) ≠ P(A | B).
사건 A의 발생유무가 사건 B의 conditional probability에 영향을 미침.
- Independent는 개별 사건이 아닌 반드시 conditional probability에서 판단해야 하며, Independent이면
P(A ∩ B) = P(A)P(B), P(A1 ∩ A2 ∩ … ∩ An) = P(A1) P(A2)… P(An).
- 쌍마다 독립(Pairwisely Independent): 여러 개의 사건들이 모두 독립 일 때.
- Mutually Exclusive Events와 Independent Event은 서로 관련이 없는 별개의 개념이다.
- Mutually Exclusive Events이면 Dependent Event이긴 하다.
- 사건 A의 확률은 사건 B가 발생했을 때 A의 조건부 확률과 사건 B가 발생하지 않았을 때 A의 조건부 확률의 합이다.
- P(A) = P(A ∩ B) + P(A ∩ BC) = P(B)P(A|B) + P(BC)P(A|BC).
- 전확률 공식(Formula of Total Probability): 표본공간 S가 사건 A1, A2, … , An의 분할로 주어진 경우, B의 조건부 확률로 B의 전체 확률을 구할 수 있다.
- P(B) = Σ (i = 1 → n) P(Ai)P(B | Ai).
- 베이즈 정리(Bayes’ Theorem): 사전에 분할된 확률 P(Ai)와 조건부 확률 P(B|Ai)를 이용하여 P(Ai|B)를 구하는 방법.
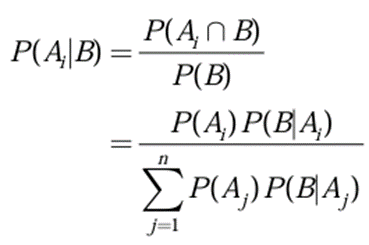
- P(Ai): 사전확률(Prior Probability), P(Ai|B): 사후확률(Posterior Probability).
'Mathematics > Probability & Statistics' 카테고리의 다른 글
| 06. 조건부 확률분포(Conditional Probability Distribution) (0) | 2024.07.06 |
|---|---|
| 05. 결합확률분포(Joint Probability Distribution) (0) | 2024.07.06 |
| 04. 기댓값(Expected value) (0) | 2024.07.06 |
| 03. 확률변수(Random Variable) (0) | 2024.07.06 |
| 01. 사건과 확률(Event and Probability) (0) | 2024.07.06 |





