엔지니어가 되고 싶은 공돌이
05. 평면벡터의 성분(Components of Plane Vector) 본문
05. 평면벡터의 성분(Components of Plane Vector)
Geca 2024. 4. 9. 15:40
5. 1 위치벡터(Position Vector)
- 위치벡터(Position Vector): 한 점(or 기준점) O를 시점으로 하는 vector OA를 점 A의 위치벡터라 부른다.
- AB = OB – OA. [AB, OB, OA is vector]
- 선분의 내분점과 외분점의 위치벡터(The Internally and Externally Dividing Points of a Triangle).

1) 선분 AB를 m : n 으로 내분(Internally Dividing Point)하는 점 P 의 position vector p는
p = (mb + na) / (m + n). [a , b, p is vector]
2) 선분 AB를 m : n 으로 외분(Externally Dividing Point)하는 점 Q 의 position vector q는
q = (mb - na) / (m - n). [a , b, q is vector]
3) 선분 AB의 중점(Middle Point) M의 position vector m은
m = (a + b) / 2. [a , b is vector]
- 삼각형의 무게중심(Center of Gravity of a Triangle).
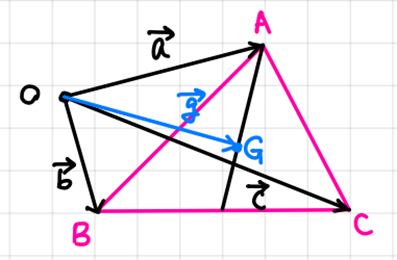
삼각형 ABC의 무게중심을 G라 하고 A, B, C, G의 positive vector를 각각 a, b, c, g라 하면
g = (a + b + c) / 3.
- OP = mOA + nOB, Trace of P. [OP, OA, OB is vector & m, n is real number]
1) 0 ≤ m ≤ 1, 0 ≤ n ≤ 1, m + n = 1.
=> segment line AB.
2) 0 ≤ m ≤ 1, 0 ≤ n ≤ 1, m + n ≤ 1.
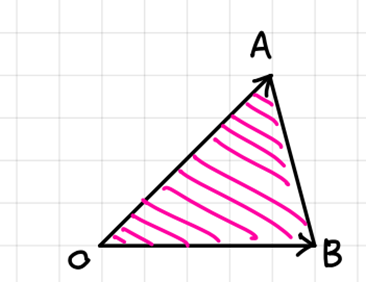
=> Perimeter and interior of triangle AOB.
3) 0 ≤ m ≤ 1, 0 ≤ n ≤ 1.
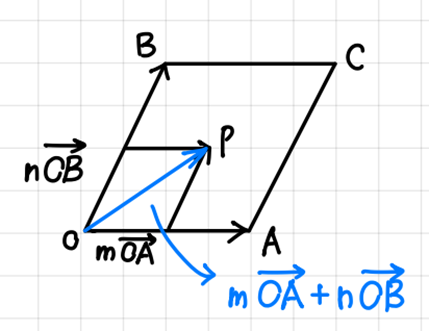
=> Perimeter and interior of a parallelogram OACB.
5 .2. 평면벡터의 성분(Components of Plane Vector)
- 원점 O를 시점으로 하고 두 점 E1(1, 0), E2(0, 1)을 각각 종점으로 하는 두 unit vector를 vector e1, vector e2 라 부른다.
- 좌표평면 위에 있는 임의의 점 A(a1 , a2)의 Position Vector를 a라 하면 a = (a1 , a2) 라 표현할 수 있고 a1 과 a2를 벡터 a의 성분(Component of a)이라 부른다.
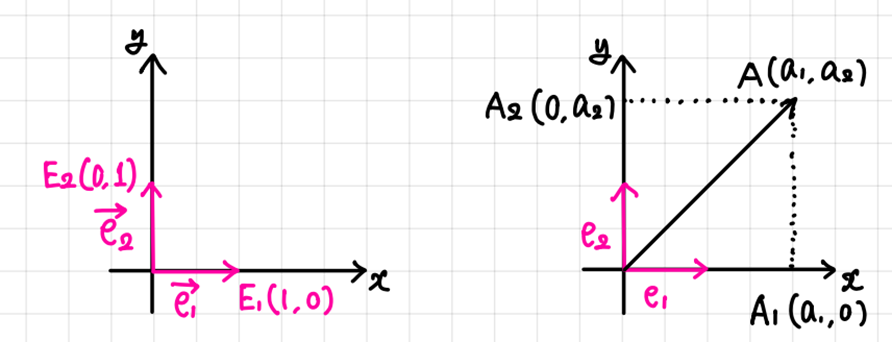
- a = (a1 , a2) 일 때, | a | = √(a12 + a22).
- a = (a1 , a2), b = (b1 , b2) 일 때 두 벡터가 서로 같을 조건은
=> a1 = b1 , a2 = b2 .
- a = (a1 , a2), b = (b1 , b2) 일 때 두 벡터의 연산은
1) a + b = (a1 + b1 , a2 + b2).
2) a – b = (a1 - b1 , a2 - b2).
3) ka = (ka1 , ka2).
'Basic Mathematics > High School_Geometry and Vector' 카테고리의 다른 글
| 07. 평면 운동(Plane Motion) (0) | 2024.04.11 |
|---|---|
| 06. 평면벡터의 내적(Dot Product of Plane Vector) (0) | 2024.04.10 |
| 04. 평면벡터의 연산(Operation of Plane Vectors) (0) | 2024.04.08 |
| 03. 평면곡선의 접선(Tangent of Plane Curve) (0) | 2024.04.07 |
| 02. 이차곡선 - 2(Conic Section - 2) (0) | 2024.04.06 |