엔지니어가 되고 싶은 공돌이
12. 정적분(Definite Integral) 본문

12. 1. 정적분(Definite Integral)
- 함수 f(x)가 구간 [a, b]에서 연속일 때,

- 정적분의 성질(Properties of Definite Integral).

- 정적분의 공식(Definite Integral Formula).
1) ∫ab kf(x) dx = k∫ab f(x) dx. [k is real number]
2) ∫ab ( f(x) ± g(x) )dx = ∫ab f(x) dx ± ∫ab g(x) dx.
3) ∫ab f(x) dx = ∫ac f(x) dx + ∫cb f(x) dx.
4) ∫ab A(x - a)(x - b) dx = -A/6 X (b - a)3.
- f(x) 가 f(-x) = f(x)를 만족할 때,
∫-aa f(x) dx = 2 ∫0a f(x) dx. -> f(x)는 짝수차항.
- f(x) 가 f(-x) = -f(x)를 만족할 때,
∫-aa f(x) dx = 0. -> f(x)는 홀수차항.
12. 2. 정적분의 치환적분법과 부분적분법(Substitution and Partial integration of Definite Integrals)
- 정적분에도 부정적분처럼 치환적분법과 부분적분법을 동일하게 적용할 수 있다.
- 다만 정적분은 그 결과가 실수이므로 치환적분과 부분적분을 할 때 a ~ b 의 범위를 고려하자.
- ∫ab f(x)g’(x) dx = [ f(x)g(x) ]ab - ∫ab f’(x)g(x) dx.
12. 3. 정적분으로 정의된 함수와 급수(Functions and Series Defined by Definite Integrals)
- 정적분으로 정의된 함수의 미분(Differential).
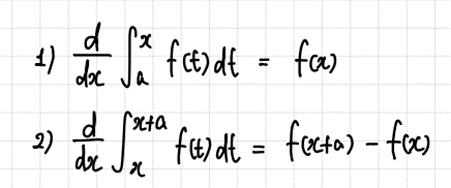
- 정적분으로 정의된 함수의 극한(Limit).
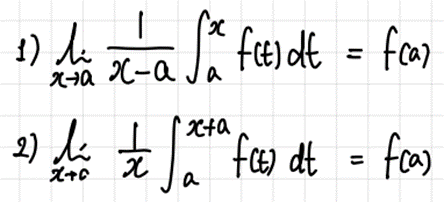
- 정적분과 급수(Series).
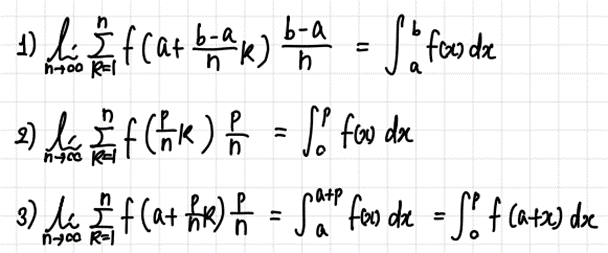
'Basic Mathematics > High School_Calculus 2' 카테고리의 다른 글
| 11. 부정적분(Indefinite Integral) (0) | 2024.04.04 |
|---|---|
| 10. 도함수의 활용 - 2 (Use of Derived Function - 2) (0) | 2024.04.03 |
| 09. 도함수의 활용 - 1 (Use of Derived Function - 1) (1) | 2024.04.03 |
| 08. 여러가지 미분법(Various Differential Calculus Methods) (0) | 2024.04.02 |
| 07. 삼각함수의 덧셈정리(Addition and Subtraction Formulas for sine and cosine and tangent) (0) | 2024.04.01 |





