엔지니어가 되고 싶은 공돌이
04. 삼각함수 - 1(Trigonometric Functions - 1) 본문
04. 삼각함수 - 1(Trigonometric Functions - 1)
Geca 2024. 3. 29. 15:57
4. 1. 각도(Angle)
- 각도(Angle)는 고정된 시작하는 선 시초선(Initial Line)으로부터, 움직이는 반 직선 동경(Radius Vector)까지의 회전한 양을 말한다.
- 시계바늘이 도는 반대방향을 양의 방향(+), 시계바늘이 도는 방향을 음의 방향(-)이라 부른다.
- x축과 y축은 좌표평면 상에서 어느 사분면에도 속하지 않는다.
- 일반각(General Angle) : 360° X n + a (n is integer & 0 ≤ a < 360°).
1) 580° = 360° X 1 + 220° (제 3사분면의 각).
2) -700° = 360° X -2 + 20° (제 1사분면의 각).
- 두 동경의 위치관계(Location relationship between the two Radius Vectors). [radius vector = A, B & n is real number]
1) 두 동경이 일치할 조건 -> A – B = 360° X n.
2) 두 동경이 일직선 위에 있고, 방향이 반대일 조건 -> A – B = 360° X n + 180°.
3) 두 동경이 x축에 대하여 대칭일 조건 -> A + B = 360° X n.
4) 두 동경이 y축에 대하여 대칭일 조건 -> A + B = 360° X n + 180°.
5) 두 동격이 직선 y = x에 대하여 대칭일 조건 -> A + B = 360° X n + 90°.
4. 2. 호도법(Circular Measure)
- 중심이 O이고 반지름의 길이가 r인 원에서 길이가 r인 호 AB를 정할 때 ∠AOB 의 크기를 1라디안(radian, θ)이라 부르고 이것을 단위로 하여 각도를 나타내는 방법을 호도법(Circular Measure)이라 부른다.
- 육십분법(Sexagesimal System)은 원의 둘레를 360° 등분하여 각도를 표현한 것을 말하고, 1°의 1/60 을 1’(분), 1’의 1/60을 1’’(초) 이라 부른다.
- radian은 실수이므로, 일반적으로 단위를 생략하여 숫자나, π로 표현한다.
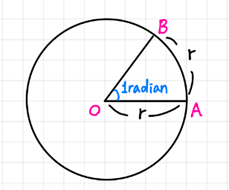
- 1radian = 180° / π = 57°17’45’’.
- 1° = (π / 180) radian.
ex) 90° = π / 2 , 180° = π , 360° = 2π.
- 일반각(General Angle) : 2nπ + θ (n is integer & 0 ≤ θ < 2π).
- l (Arc Length, 호의 길이) = rθ.
- S (Area of Circular Sector, 부채꼴의 넓이) = 1/2rl = 1/2r2θ.
'Basic Mathematics > High School_Calculus 2' 카테고리의 다른 글
| 06. 삼각함수의 그래프(Graphs of Trigonometric Functions) (0) | 2024.03.31 |
|---|---|
| 05. 삼각함수 - 2(Trigonometric Functions - 2) (0) | 2024.03.30 |
| 03. 지수함수와 로그함수의 미분(Differentiation of Exponential and Logarithmic Functions) (0) | 2024.03.29 |
| 02. 로그함수(Logarithmic Function) (0) | 2024.03.28 |
| 01. 지수함수(Exponential Function) (0) | 2024.03.28 |




