엔지니어가 되고 싶은 공돌이
06. 삼각함수의 그래프(Graphs of Trigonometric Functions) 본문
06. 삼각함수의 그래프(Graphs of Trigonometric Functions)
Geca 2024. 3. 31. 22:52
6. 1. 삼각함수의 그래프(Graphs of Trigonometric Functions)
- 주기함수(Periodic Function): 상수함수가 아닌 함수에서 f(x + p) = f(x).
- Graph of y = sin θ.
1) 정의역(Domain): 실수 전체의 집합.
2) 치역(Codomain): -1 ≤ y ≤ 1.
3) 2π 를 주기로 하는 주기함수이다.
4) y = sin θ 의 그래프는 원점에 대하여 대칭이다.

- Graph of y = cos θ.
1) 정의역(Domain): 실수 전체의 집합.
2) 치역(Codomain): -1 ≤ y ≤ 1.
3) 2π 를 주기로 하는 주기함수이다.
4) y = cos θ 의 그래프는 y 축에 대하여 대칭이다.

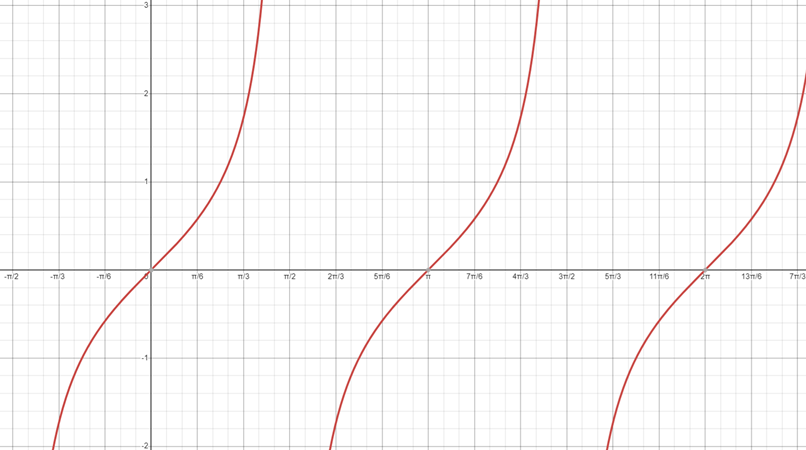
- Graph of y = tan θ.
1) 정의역(Domain): nπ + π/2 (n is integer)를 제외한 실수 전체의 집합.
2) 치역(Codomain): 실수 전체의 집합.
3) π 를 주기로 하는 주기함수이다.
4) y = tan θ의 그래프는 원점에 대하여 대칭이다.
5) 점근선(Asymptote)은 θ = nπ + π/2 (n is integer) 이다.
- Graph of y = a sin bx (or y = acos bx).
1) y = sin x (or y = cos x) 의 그래프를 y축의 방향으로 | a |배, x축의 방향으로 | 1/b |배 확대 또는 축소한 그래프이다.
2) 최대값(Max): | a |, 최솟값(Min): - | a |, 주기(Period): 2π / | b |.
- Graph of y = a sin (bx + c) + d (or y = a cos (bx + c) + d).
1) y = a sin bx (or y = a cos bx) 의 그래프를 x축의 방향으로 -c/b만큼, y축의 방향으로 d만큼 평행이동한 그래프이다.
2) 최대값(Max): | a | + d, 최솟값(Min): - | a | + d, 주기(Period): 2π / | b |.
- Graph of y = a tan bx.
1) y = tan x의 그래프를 y축의 방향으로 | a |배, x축의 방향으로 | 1 / b |배 확대 또는 축소한 그래프이다.
2) 최대값(Max), 최솟값(Min)은 없다(X), 주기(Period): π / | b |, 점근선의 방정식: x = 1/b(nπ + π/2).
- Graph of y = a tan (bx + c) + d.
1) y = a tan bx 의 그래프를 x축의 방향으로 -c/b만큼, y축의 방향으로 d만큼 평행이동한 그래프이다.
2) 최대값(Max), 최솟값(Min)은 없다(X), 주기(Period): π / | b |
- 절댓값 기호가 포함된 삼각함수의 주기와 최대 최소.
(Period, Maximum Value, Minimum Value of Trigonometric Functions with Absolute Value Symbols)
1) y = | a sin bx |.
- 최대값(Max): | a |, 최솟값(Min): 0, 주기(Period): π / | b |.
2) y = | tan bx |.
- 최대값(Max): 없다, 최솟값(Min): 0, 주기(Period): π / | b |.
6. 2. Maximum and Minimum of Expressions Containing Trigonometric Functions
- 절댓값(Absolute Values)기호를 포함하면, 삼각함수를 t로 치환하고 t에 대한 그래프를 그린다. 이 때, t의 값의 범위에 주의.
- 이차식(Quadratic Equations)의 꼴이면 sin2 x + cos2 x = 1 등의 공식을 이용해 한 종류의 삼각함수로 변형하고, 삼각함수를 t로 치환하고, t에 대한 그래프를 그린다. 이 때, t의 값의 범위에 주의.
- 분수식(Fractional Expressions)의 꼴이면 삼각함수를 t로 치환하고 t에 대한 그래프를 그린다. 이 때, t의 값의 범위에 주의.
- sin x = t (-1 ≤ t ≤ 1) , cos x = t (-1 ≤ t ≤ 1).
6. 3. 삼각방정식과 삼각부등식(Trigonometric Equation and Trigonometric Inequality)
- 삼각방정식(Trigonometric Equation): 삼각함수의 각의 크기를 미지수로 하는 방정식.
- 삼각방정식의 풀이(Solving Trigonometric Equation).
1) 주어진 방정식을 삼각함수 = t (t is real number)의 형태로 풀어낸다.
2) 삼각함수의 그래프와 y = t의 직선을 겹치게 그린다.
3) 삼각함수의 그래프와 직선의 교점의 x좌표가 해이다.
- 삼각부등식(Trigonometric Inequality): 삼각함수의 각의 크기를 미지수로 하는 부등식.
- 삼각부등식의 풀이(Solving Triangle Inequality).
1) 주어진 방정식을 삼각함수 (부등호) t (t is real number)의 형태로 풀어낸다.
2) 삼각함수의 그래프와 y = t의 직선을 겹치게 그린다.
3) 삼각함수의 그래프와 직선의 교점의 x좌표를 찾고 부등호에 맞게 해의 범위를 구한다.
'Basic Mathematics > High School_Calculus 2' 카테고리의 다른 글
| 08. 여러가지 미분법(Various Differential Calculus Methods) (0) | 2024.04.02 |
|---|---|
| 07. 삼각함수의 덧셈정리(Addition and Subtraction Formulas for sine and cosine and tangent) (0) | 2024.04.01 |
| 05. 삼각함수 - 2(Trigonometric Functions - 2) (0) | 2024.03.30 |
| 04. 삼각함수 - 1(Trigonometric Functions - 1) (1) | 2024.03.29 |
| 03. 지수함수와 로그함수의 미분(Differentiation of Exponential and Logarithmic Functions) (0) | 2024.03.29 |