엔지니어가 되고 싶은 공돌이
02. 로그함수(Logarithmic Function) 본문

2. 1. 로그함수와 그래프(Logarithmic Function and Graph)
- y = loga x (a > 0, a ≠ 1, x > 0).
- y = ax 의 역함수이다.

( a > 1 )
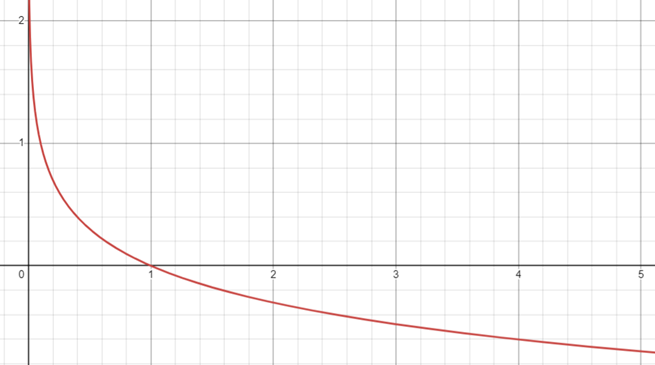
( 0 < a < 1 )
- 로그함수 그래프의 성질(Properties of Logarithmic Function Graphs).
1) 정의역(Domain)은 양의 실수 전체의 집합이고, 치역(Codomain)은 실수 전체의 집합이다.
2) 그래프는 (1, 0), (a, 1)를 지나고, y축이 점근선(Asymptote)이다.
3) y = log1/a x 그래프와 y = loga x 그래프는 x축에 대하여 대칭이다.
- y = loga x 그래프를 x축으로 p만큼, y축으로 q만큼 평행이동 -> y = loga (x – p) + q.
정의역은 x > p 이고, 점근선의 방정식은 x = p 이다.
- y = loga x 그래프를 x축 대칭이동 하면 y = loga (1/x) , y축 대칭이동하면 y = loga (-x) , 원점 대칭이동하면 y = loga (-1/x) .
- 로그함수의 대소를 비교할 때는 밑을 같게 한 후 진수를 비교한다.
2. 2. 로그함수의 최대최소(Max and Min of Logarithmic Functions)
- 정의역이 p ≤ x ≤ q일 때, 로그함수 y = loga x 의 최대 최소는 다음과 같다.
1) a > 1 일 때 증가함수이므로 x = p에서 최솟값, x = q에서 최댓값을 갖는다.
2) 0 < a < 1 일 때 감소함수이므로 x = p에서 최댓값, x = q에서 최솟값을 갖는다.
- y = (loga x)2 + p(loga x) + q 의 형태는 loga x 를 t와 같은 한 문자로 치환하여 최대최소를 구한다.
- y = loga f(x)의 경우 a > 1이면 f(x) 가 최대일 때 함수값도 최대이고, f(x)가 최소일 때 함수값도 최소이다.
0 < a < 1이면 f(x) 가 최소일 때 함수값이 최대이고, f(x)가 최대일 때 함수값은 최소이다.
- 지수에 로그가 있는 함수면 양변에 로그를 취한다.
2. 3. 로그방정식(Logarithmic Equation)
- 로그방정식(Logarithmic Equation): 로그의 진수 또는 밑에 변수를 포함하고 있는 방정식.
- 로그방정식의 풀이(Solving Logarithmic Equations).
1) loga f(x) = b -> f(x) = ab .
2) 밑이 같다면 -> 진수가 같아야 한다.
3) 밑이 같지 않으면 -> 밑부터 같게 만들고 방정식을 푼다.
4) 진수가 같으면 -> 밑이 같거나 진수가 1이다.
5) loga x 가 반복되면 loga x = t로 치환하여 푼다.
6) 지수에 로그가 있으면 양변에 로그를 취하여 푼다.
- 밑은 0보다 크고 1이면 안되고, 진수는 0보다 커야 한다.
2. 4. 로그부등식(Logarithmic Inequality)
- 로그부등식(Logarithmic Inequality): 로그의 진수 또는 밑에 변수를 포함하고 있는 부등식.
- a > 1 일 때, loga f(x) > loga g(x) 이면 f(x) > g(x) 이고, 0 < a < 1 일 때, loga f(x) > loga g(x) 이면 f(x) < g(x) 이다.
- 로그부등식의 풀이(Solving Logarithmic Inequality).
1) 밑이 같다면 -> 진수를 비교.
2) 밑이 같지 않으면 -> 밑부터 같게 만들고 부등식을 푼다.
3) loga x 가 반복되면 loga x = t로 치환하여 푼다.
4) 지수에 로그가 있으면 양변에 로그를 취하여 푼다.
'Basic Mathematics > High School_Calculus 2' 카테고리의 다른 글
| 06. 삼각함수의 그래프(Graphs of Trigonometric Functions) (0) | 2024.03.31 |
|---|---|
| 05. 삼각함수 - 2(Trigonometric Functions - 2) (0) | 2024.03.30 |
| 04. 삼각함수 - 1(Trigonometric Functions - 1) (1) | 2024.03.29 |
| 03. 지수함수와 로그함수의 미분(Differentiation of Exponential and Logarithmic Functions) (0) | 2024.03.29 |
| 01. 지수함수(Exponential Function) (0) | 2024.03.28 |