엔지니어가 되고 싶은 공돌이
02. 급수와 함수의 전개(Expansion of Series and Functions) 본문
Mathematics/Numerical Analysis
02. 급수와 함수의 전개(Expansion of Series and Functions)
Geca 2024. 7. 12. 12:56
2. 1. 급수와 함수의 전개(Expansion of Series and Functions)
- 급수(Series): a1 + a2 + … + an + … .
- i가 유한하면 Finite Series, i가 무한하면 Infinite Series 라 부른다.
- 멱급수(Power Series).
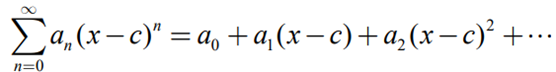
(x - c)에 대한 멱급수(Power Series)라고 부른다.
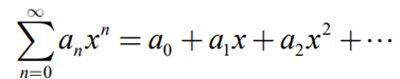
x에 대한 멱급수(Power Series)라고 부른다.
- Talyor Series: 함수 f(x)를 모른다고 할 때, x = c 에 대하여 f(c) , f’(c) , f’’(c) … 이 가능하고 그 값을 알 수 있으면 모르는 함수 f(x)를 근사적으로 구할 수 있다.
- Talyor Series는 c에 근접한 점 p의 f(p)를 구하거나, f(x)를 다항식의 합으로 표현하거나, 무리수의 값을 정확하게 계산할 때 사용한다.
- n차 Taylor 전개(nth Taylor Expansion)
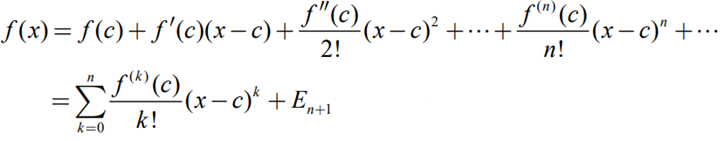
- 1차근사식, 2차근사식(First-Order Taylor Approximation, Second-Order Taylor Approximation).
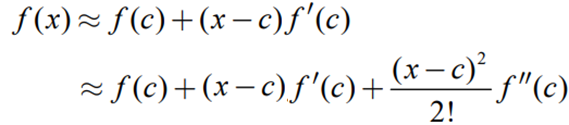
- 매클로닌 급수(Maclaurin Series): Taylor Series 에서 c = 0인 경우.
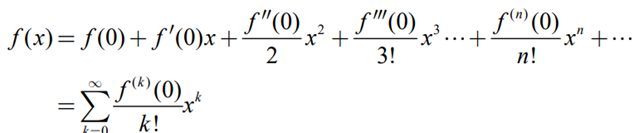
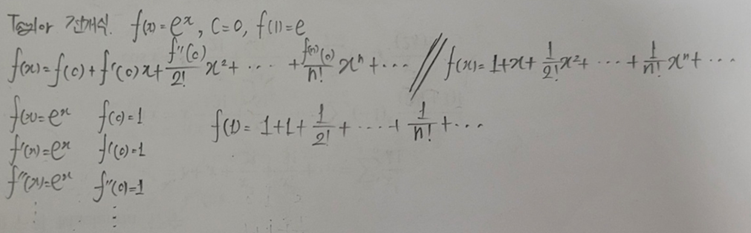
'Mathematics > Numerical Analysis' 카테고리의 다른 글
| 06. 선형방정식의 반복법(Iteration Method of Linear Equation) (0) | 2024.07.12 |
|---|---|
| 05. 노름(Norm) (0) | 2024.07.12 |
| 04. LU 분해법과 숄레스키 방법(LU Decomposition Method and Cholesky Method) (0) | 2024.07.12 |
| 03. 행렬(Matrix) (0) | 2024.07.12 |
| 01. 수와 오차(Number and Error) (0) | 2024.07.12 |
Comments





